السرعة اللحظية

         الذي توضحه الصورة في الشكل 1)) هي حركة سقوط جسم . هذه الصورة تبين موضع الكرة على فترات زمنية منتظمة ، وقد تم التقاطها باستخدام ضوء مضيئ تتكرر ومضاته بنفس المعدل ، ولنفرض أن tΔ (وتقرأ دلتا تي) هي الفترة الزمنية بين ومضتين متتاليتين. لاحظ أن الكرة تتسارع أثناء السقوط ، وهذا واضح من زيادة المسافة خلال كل فترة زمنية تالية. ولنناقش الآن طريقة تعيين سرعة الكرة عند مرورها بنقطة ما ولتكن C ، وتسمى السرعة عند نقطة معينة بالسرعة اللحظية عند تلك النقطة.

((1

من الواضح أن أتجاه السرعة هنا رأسي إلى أسفل لأنه هو نفس اتجاه الحركة. ولإيجاد قيمة تقريبية لمقدار سرعة الكرة عند C يمكننا حساب السرعة المتوسطة بين النقطتين A و B . لنسمي إحداثي قياس موضع الكرة y. إذن ، عندما تنتقل الكرة من A إلى B تكون إزاحتها yΔ. وحيث ان tΔ هو الزمن بين ومضتين متتاليتين من الضوء فإن الزمن الذي تستغرقه الكرة للانتقال من A إلى B يكون أيضاً tΔ. وعليه ، فمتوسط سرعة الكرة في المنطقة من A إلى B هو:

لكن هذه ليست سرعة الكرة عند C بالضبط لأن السرعة تتزايد باستمرار . وإذا زادت سرعة الومضات الضوئية ( أي إذا قلت tΔ) ستصبح صور الكرة اكثر قرباً من بعضها البعض وتصبح النقطتان A و B أكثر قرباً إلى C. فإذا ما أجرينا حساباتنا بالنسبة لهاتين النقطتين الجديدتين A وB فإن السرعة المتوسطة التي نحصل عليها لابد أن تكون أقرب إلى سرعة الكرة عند C من القيمة الأول السابق حسابها .

وبهذه يمكننا أن نتخيل حالة تكون فيها الومضات الضوئية من السرعة بحيث تقترب الفترة الزمنية بين الومضات من الصفر ، وهو ما نمثله هكذا 0→tΔ. وعندئذ تصبح  النقطتان A  و B قريبتين جداً من C وبدرجة تمكننا من اعتبار ان السرعة المتوسطة التي نحسبها مساوية تماماً للسرعة عند C وبدرجة تمكننا من اعتبار أن السرعة المتوسطة التي نحسبها مساوية تماماً للسرعة عند C. وعندئذ تسمى السرعة عند C  بالسرعة اللحظية عند هذه النقطة وتمثل بالحرف v (بدون الشرطة العلوية). وبدلالة الطريقة العلمية السابق شرحها. تعرف السرعة اللحظية إذن كالتالي:

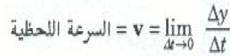
ويقرأ الرمز 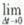 هكذا ( في حالة الحدية عندما تقترب tΔ من الصفر) . هذا التعريف هو التمثيل الرياضي للطريقة العلمية التي تكون فيها tΔ من الصفر بحيث تصبح السرعة المتوسطة بين A و B مساوية أساساً للسرعة اللحظية عند C , وبأي ضباطية نريد .

هناك علاقة هامة بين مقداري السرعة اللحظية عند نقطة مثل C ومعدل الحركة عند C إذا كانت tΔ صغيرة جداً لن يتمكن الجسم من تغيير اتجاه حركته بدرجة محسوسة خلال الزمن الذي يستغرقه للانتقال من A إلى B ، ونتيجة لذلك تكون المسافة المستقيمة من A إلى B مساوية للمسافة التي يقطعها الجسم عند انتقاله من A إلى B , وحيث ان المسافة المقطوعة والإزاحة متساوي المقدار فإن السرعة اللحظية ومعدل الحركة عند C متساويان في المقدار أيضاً.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل