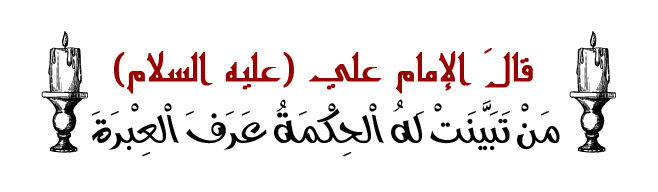
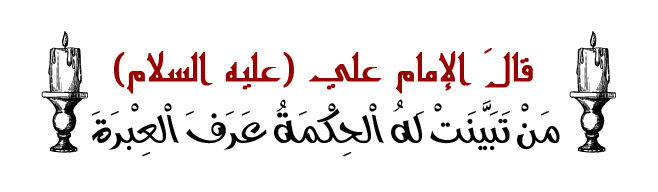

 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-2-2018
Date: 21-2-2018
Date: 25-2-2018
|
Born: 26 September 1927 in Horwich, Lancashire, England
Died: 4 June 2008 in Southampton, England

Brian Griffiths attended Leigh grammar school, completing his school studies in 1945 and so just missing having to serve in World War II. He was an undergraduate at Manchester University where he studied mathematics and was awarded a B.Sc. He continued to undertake research at Manchester under the supervision of Max Newman. He was awarded an M.Sc. then in 1952 a Ph.D. for his thesis Local Topological Invariants. In his thesis he studied "homotopy manifolds," homotopy analogues of the generalized manifolds which had earlier been investigated by Raymond Wilder. He published three papers based on the ideas in his thesis Local topological invariants (1953), A mapping theorem in "local" topology (1953), and A contribution to the theory of manifolds (1954).
After the award of his doctorate, Griffiths was appointed to the University of Aberdeen. While in Aberdeen he met Catherine whom he later married; they had three children Hannah, Adam and Joe. He spent the years 1956-58 at the Institute for Advanced Study at Princeton. From Aberdeen, Griffiths went to the University of Bristol and then to the University of Birmingham. There he became a colleague of Peter Hilton and the two ran an in-service course for teachers of mathematics at Birmingham University in 1961-62. The course looked at how classical mathematics was being presented in new ways in universities and discussed how such changes might change mathematics teaching in schools. This project led to Hilton and Griffiths publishing A comprehensive textbook of classical mathematics in 1970. Here are a few quotations from the book to illustrate what the authors were trying to do:-
We do not forget, however, that 'the most important existence theorem in mathematics is the existence of people'.
... mathematical ideas are not communicated from mathematician to mathematician in extremely precise form ....
One of us believes ..., while the other believes the opposite: but both agree that it would be folly to insist here on a single viewpoint.
... if the object of teaching is to communicate, rather than to give aesthetic satisfaction to the expositor, then we must be prepared to put pedagogical techniques above mere logic ....
... whatever mathematics is, it is not the quest for absolute certainty.
K E Hirst, reviewing the book, explains that the authors take a:-
... second look at many ideas, albeit in different contexts, for those who have met them in school or as undergraduates. ... Thus a picture is painted of classical mathematics as a network of ideas, and of more recent developments as tools to make further connections and offer new insights, as well as having importance in their own right. ... As well as illuminating classical mathematics, the book also provides a way forward into more recent topics, clearly demonstrating that subjects like topology and modern algebra have firm classical roots, unlike many expositions which give the impression of self-contained inventions which have superseded older mathematics. __The authors attach considerable importance to the "spiral approach" whereby a given idea returns again and again as the context merits it. This is contrasted with many apparently linear expositions which, the authors emphasise, differ radically from the way in which ideas in mathematics are actually assimilated by mathematicians.
Before this book was published, Griffiths spent the year 1963-64 at the Courant Institute in New York. He returned to England in 1964 to take up an appointment as Professor of Pure Mathematics at Southampton University. He was to continue to hold this post for 28 years until he retired in 1992. During these years he published articles on topology and also took a deep interest in mathematical education, publishing important and influential article on that topic. For example his work on topology included the text Surfaces published by Cambridge University Press. The first English edition appeared in 1976, with a German translation two years later. A second edition appeared in 1981 and Griffiths writes in the Preface:-
Several reviewers and correspondents have shown a warm interest in the book and made suggestions for improving it; where possible I have altered the original text accordingly.
This tells us much about Griffiths, for few authors react in this fashion to criticisms of their work. In fact we can see more clearly why he reacted in this way when we read one of the reviews he wrote. In 1980 R E Edwards published A formal background to mathematics. Griffiths reviewed the book for the Bulletin of the American Mathematical Society and we quote part of the review which gives considerable insight in Griffths own approach [2]:-
Before I can review this unusual book adequately, it is necessary to consider how academic mathematicians (such as readers of this Bulletin) have gradually come to expect mathematics books to be written in a standard way. About a century ago, for example, books on Physics were appearing in Britain, written by confident authors who declared in enthusiastic Prefaces that their readers could now understand the mysteries of the Universe, God's handiwork, etc. By the 1920's the style had changed and a different type of author would say in his Preface 'This book contains all that is necessary for the B.Sc. Examinations of ... '. In Mathematics, as well as Physics and other disciplines, the Enthusiast still writes, but he usually conforms to the American euphemism of the 'Reward Structure'; his readership may not be working for B.Sc. degrees, but they are in a hurry and want him to get cracking. They want the gold nuggets of the mathematical mine, without the view from the mountain, or disquisitions upon the systems fed by the gold. Among other things, therefore, they are unlikely to dwell on his Preface (especially if it is long and complex), and they expect a flow of information that is organised and assembled in a conventional way, to get to the point as quickly as possible. Of course, there is also an unspoken convention as to what this 'point' is, and the convention is reinforced by almost every new book that appears in the rapid growth of mathematics publishing during the past40 years. A few books appear which have a different 'point', and this is one of them. Like the early Physics books, it aims to put the gold nuggets of the mathematics into a synoptic view. It is a work of Mathematics Education, which is a more complex affair than 'just' Mathematics. ...
Also, and with humble diffidence, the author does something which is rarely if ever done elsewhere and looks at various books which deal with particular topics. He analyses statements made by them; and this type of criticism, if pursued more widely with similar courtesy and responsibility, could be good for us all for two reasons. First, the criticised authors can benefit because we have no process institutionalised in the mathematical community for deciding whether books are good or bad (there is the writing of reviews, but these rarely deal with the detailed criticism that can come from usage of books, and it is a standard practice that reviewers do not criticise in the manner of (say) drama-critics). Second, teachers or intending teachers need training in how to look at books, deluged as they are by publishers wanting them to adopt texts which, with a wrong choice, can result in heavy investment in an unsuitable book; yet few mathematics or education courses give any training in the skills of reading a book, let alone assessing it.
We give the titles of a few of his mathematical education article which give an overview of his interests in that topic: Pure mathematicians as teachers of applied mathematicians (1968); Mathematics Education today (1975); Successes and failures of mathematical curricula in the past two decades (1980); Simplification and complexity in mathematics education (1983); The implicit function theorem: technique versus understanding (1984); A critical analysis of university examinations in mathematics (1984); Cubic equations, or where did the examination question come from? (1994); The British Experience of Teaching Geometry since 1900 (1998); and The Divine Proportion, matrices and Fibonacci numbers (2008).
His influence on mathematical education was certainly not restricted to his publications. He was deeply involved in the 'School Mathematics Project', he served as chairman of the 'Joint Mathematical Council', and chaired the steering group for the 'Low Attainers Mathematics Project' from 1983 to 1986. This project became the 'Raising Achievement in Mathematics Project' in 1986 and he chaired this from its foundation to 1989.
Outside mathematics the Griffiths family suffered hardships and joys [1]:-
During much of this time, Catherine and Brian faced difficult problems at home, for both their sons suffered from cystic fibrosis and required extensive care. The death of the younger son, Joe, prevented Brian from giving an invited talk on mathematics education to the 1970 International Congress of Mathematicians, and the elder, Adam, died when studying for a DPhil at Oxford. Nonetheless, the Griffiths were always generous hosts and took great care to see that newcomers to the department were comfortably settled in Southampton. Their house was always one of music. Catherine was a piano teacher and their daughter, Hannah, a cellist. However, only after retirement in 1992, could Brian find time to practise his violin and play in a local string orchestra and two string quartets.
A conference in Southampton on 21 June 2008 was dedicated to the memory of Griffiths who had died suddenly just over two weeks before. He was described in the programme as:-
A fine mathematician, a good friend to mathematics education, and a supremely nice person always willing to share his expertise.
Articles:



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|