


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-3-2016
Date: 8-9-2020
Date: 17-8-2020
|
Tidal scattering
Tidal scattering is another mechanism that can affect the internal structure of a significant fraction of the stars around the MBH. Tidal scattering does not require a very high stellar density, since it is driven by the global response of the system to the existence of a mass sink, the MBH, in its center.
Some of the mass that feeds the growth of a MBH in a galactic center is supplied by tidal disruption of stars that are scattered into low angular momentum orbits (‘loss-cone’ orbits). When the MBH mass is small enough that the tidal radius is larger than the event horizon, rt > rs, the star is tidally disrupted before crossing the event horizon. The accretion of stellar debris from such events may give rise to observable ‘tidal flares’ (Frank and Rees 1976). Significant theoretical efforts have gone into estimating the rates, timescales, luminosities and spectra of the flares (e.g. Ulmer et al 1998,Magorrian and Tremaine 1999, Ayal et al 2000), in the hope that they can be used to detect MBHs in the centers of galaxies. There is today only marginal evidence for the detection of such flares (e.g. Renzini et al 1995, Komossa and Bade 1999, Komossa and Greiner 1999).
The effect of the MBH's tidal field is not limited to tidal disruption. For every star that is actually disrupted, there are stars with rp > rt that narrowly escape tidal disruption by the central BH after being subjected to extreme tidal distortion, spin-up, mixing and mass loss, which may affect their evolution and appearance (Alexander and Livio 2001). Figure 1.1 shows a Smoothed Particle Hydrodynamics (SPH) simulation of a star passing by a MBH just outside the tidal disruption radius. To leading order, the effects of tidal scattering are a function of the penetration parameter β = rt/rp only, and are independent of the MBH mass,
 (1.1)
(1.1)
For a parabolic orbit and for M● >> M*. As will be argued later, a large fraction of these ‘tidally scattered’ stars survive eventual orbital decay and disruption, and so remain in the system as relics of the epoch of tidal processes even after the MBH becomes too massive for tidal disruption.
Dynamical analyses of the scattering of stars into the loss-cone orbits (Light man and Shapiro 1977, Magorrian and Tremaine 1999) show that tidally disrupted stars in galactic nuclei are typically on slightly unbound orbits relative to
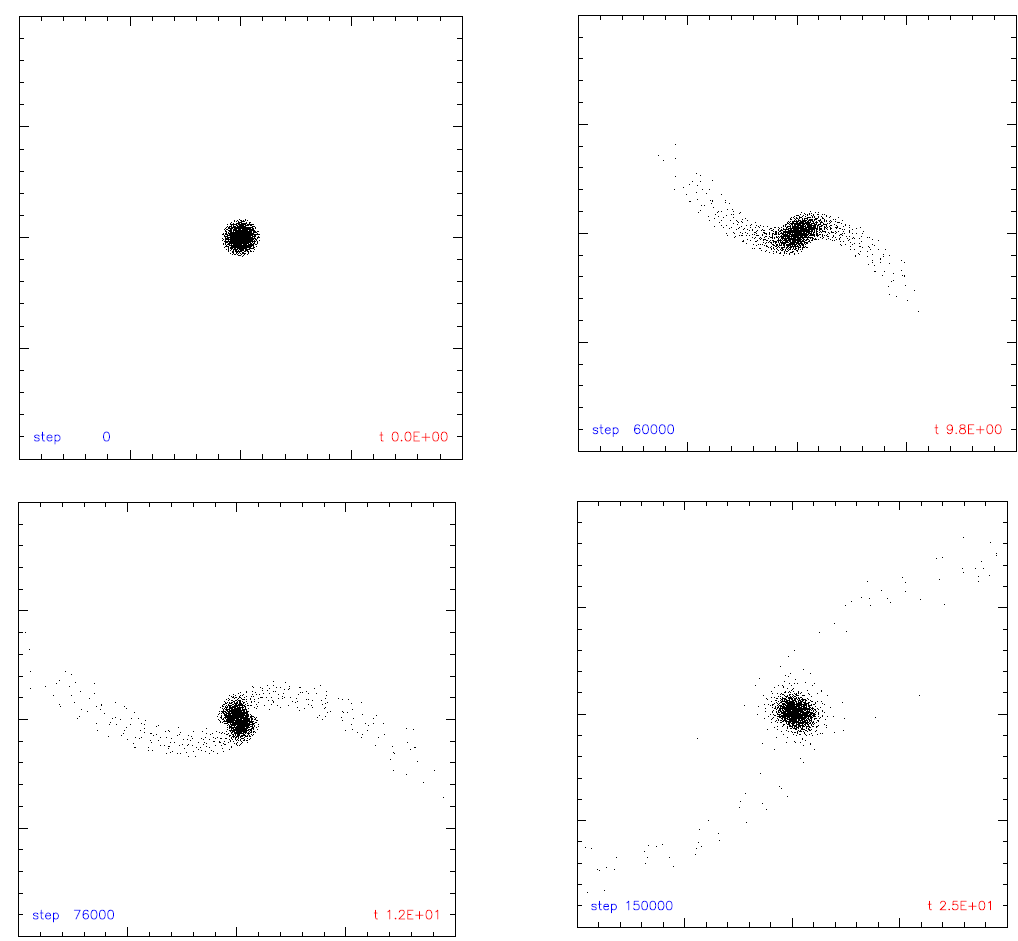
Figure 1.1. Snapshots from a Smoothed Particle Hydrodynamics (SPH) simulation of a star undergoing an extreme non-disruptive tidal interaction (‘tidal scattering’) as it passes near a massive black hole. Time is measured in units of the star's dynamical timescale. The star passes near the black hole (located outside the frame) on a parabolic orbit with a peri-distance 1.5 times larger than the tidal disruption distance. Shortly after periapse passage (t = 12) the star appears to be on the verge of breaking in two. However, by the end of the simulation, the two fragments coalesce, leaving a distorted, mixed and rapidly rotating bound object.
the MBH and that they are predominantly scattered into the loss cone from orbits at the radius of influence of the BH, rh. The scattering operates on a timescale that is shorter than the dynamical timescale, and so the stars are scattered in and out of the loss-cone several times during one orbital period. Because of gravitational focusing, the cross section for scattering into a hyperbolic orbit with periapse ≤ rp scales as rp, and not as r2p (Hills 1975, Frank 1978), and so the number of stars with rt ≤ rp ≤ 2rt equals the number of stars that were disrupted by the MBH.
Tidal disruption is an important source of mass for a low-mass MBH that accretes from a low-density galactic nuclear core, where mass loss from stellar collisions is small (e.g. Murphy et al 1991). For the MBH in the Galactic Center, the total mass in disrupted stars can be 0.25M● or even higher (Freitag and Benz 2002). Since the enclosed stellar mass within rh is also ∼M●, the tidally scattered stars comprise a significantly high fraction of the stellar population within the radius of influence of the MBH.
After the first periapse passage, the tidally scattered star will be on a very eccentric orbit with a maximal radius (apoapse) of < 2rh. Since the two-body interactions that scattered it into the eccentric orbit operate on a timescale that is shorter than the orbital period, there is a significant chance that the star will be scattered again off the orbit and miss the MBH. The chance of this happening is further increased by the Brownian motion of the MBH relative to the dynamical center of the stellar system. The amplitude of the Brownian motion is much larger than the tidal radius, and it proceeds on the dynamical timescale of the core (Bahcall and Wolf 1976), which is comparable to the orbital period of the tidally disturbed stars. The orbits of the tidally scattered stars take them outside of rh, where they are no longer affected by the relative shift between the BH and the stellar mass. Therefore, on re-entry into the volume of influence, their orbit will not bring them to the same periapse distance from the MBH. Both the random motion of the MBH and the scattering off the loss-cone by two-body interactions are expected to increase the survival fraction to a significantly high value. More detailed calculations, which integrate over the orbital distribution, are required to confirm these qualitative arguments.
Rough estimates (Alexander and Livio 2001) indicate that the Galactic Center may harbor 104−5 tidally scattered stars. These stars are expected to be on highly eccentric orbits, and so there may be observable correlations between high orbital eccentricity and the stellar properties.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|