


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 16-7-2017
Date: 2-12-2020
Date: 12-12-2016
|
The matter equations
We first remind the reader of classical physics. We consider atoms which we distinguish by an index μ and which are localized at the space points xμ. By means of a simple model we treat the motion of an electron within an atom by assuming that it is elastically coupled to the atomic nucleus. The displacement of the electron from its equilibrium position at the nucleus will be denoted by ξμ. With it a dipole moment
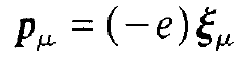 (1.1)
(1.1)
is connected. In classical physics the deviation ξμ of the electron with charge -e and mass m obeys the equation of motion
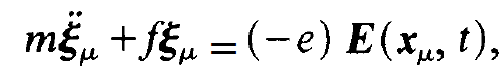 (1.2)
(1.2)
where f is Hook's constant. The electric field strength E is taken at the position xμ of the atom (fig. 1.1). Assuming E in the form of an harmonic oscillation,
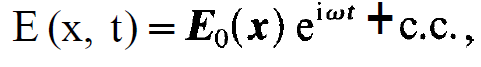 (1.3)
(1.3)
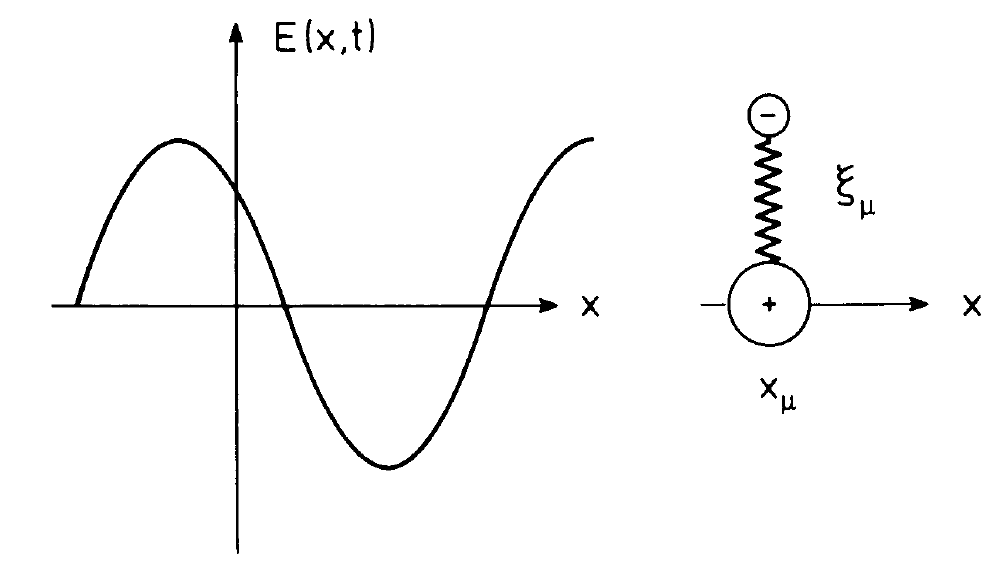
Fig. 1.1. The electric field strength E(x, t) (left part) hits an atomic dipole at space point xλ and with its elongation ξμ (right part).
we can solve (1.2) immediately
 (1.4)
(1.4)
where we have used the abbreviation
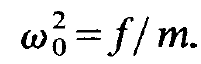 (1.5)
(1.5)
Inserting this result into (1.1) we recognize that the dipole moment pμ of the atom μ is connected with the electric field strength by a constant factor a, the polarizability of the atom,
 (1.6)
(1.6)
An inspection of (5.13) reveals that the polarizability is explicitly given by
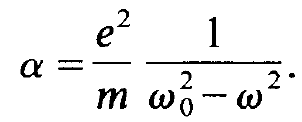 (1.7)
(1.7)
Because the polarization of the medium is the sum over the dipole moments per unit-volume it follows from (1.6) that P is proportional to E. The second derivative of P with respect to time occurs, the net effect of the polarization is a change of the effective velocity of light in the medium. Of course, what we have presented up to now is nothing but conventional dispersion theory. This theory is not able to represent laser action adequately, however. Rather we have to deal with the quantum mechanical processes. To this end we assume that only two energy levels within an atom participate at the interaction between the atom and the light field. We denote the electronic coordinate by ξ. With respect to the electron we treat the problem fully quantum mechanically and therefore start from the Schrodinger equation
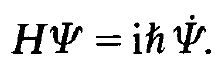 (1.8)
(1.8)
In it the Hamiltonian H is composed of the unperturbed operator H0 and the operator of the external perturbation Hs
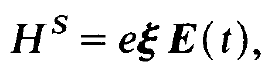 (1.9)
(1.9)
i.e.
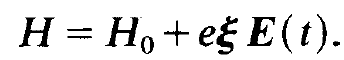 (1.10)
(1.10)
H0 refers to the unperturbed motion of the electron in the field of its atomic nucleus. In the following we shall assume that the corresponding quantum mechanical problem
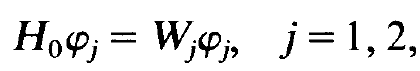 (1.11)
(1.11)
has been solved already, i.e. that we know the wave functions φj and their energies Wj. In we got to know how to treat the Schrodinger equation (1.8). To this end we construct the wanted wave function Ψ as a superposition of the unperturbed wave functions φ1 and φ2. In other words, we shall assume in the following that the interaction between the electron and the electric field strength E is only of importance for the two levels under consideration. This may be justified by the fact that the frequency of the electric field strength is in or close to resonance with the frequency of the electronic transition between the corresponding two levels so that the electric field strength stimulates transitions between levels 2 and 1. In order to determine the coefficients c, and c, we insert as usual the hypothesis
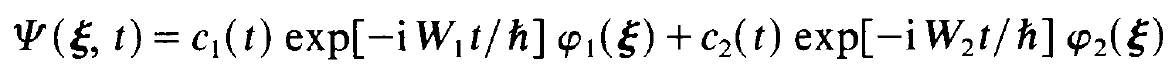 (1.12)
(1.12)
in (1.8) and multiply the resulting equation by φ1 and φ2, respectively. We then integrate over the electron coordinate ξ and obtain the equations
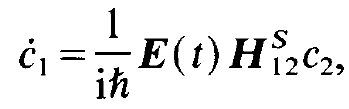 (1.13)
(1.13)
 (1.14)
(1.14)
In order to simplify these equations we have introduced the matrix elements as follows:
 (1.15)
(1.15)
where ⍵mn is given by
 (1.16)
(1.16)
Furthermore we have assumed that the atom does not possess a static dipole moment so that
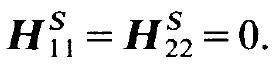 (1.17)
(1.17)
When we know the coefficients c1 and c2, which can in principle be obtained by solving eqs. (1.13) and (1.14), we may calculate various important expectation values, for instance that of the atomic dipole moment
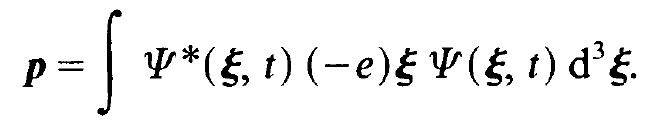 (1.18)
(1.18)
In order to simplify the notation we consider only one selected atom so that we neglect the index μ for the moment being. We have introduced that index above in order to distinguish the atoms. The expectation value of the dipole moment p replaces the classical dipole moment (1.6). Thus, if we can calculate p, we may determine the polarization P of the medium so that our task to calculate the source term of the wave equation will be solved. Inserting Ψ, eq. (1.12), in (1.18) and using the relations (1.17) we obtain
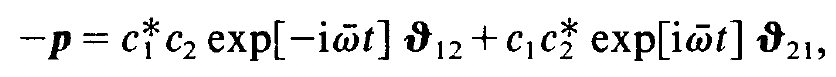 (1.19)
(1.19)
where we have used the abbreviations
 (1.20)
(1.20)
and
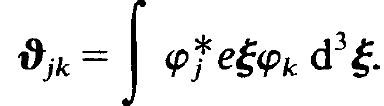 (1.21)
(1.21)
From this result it transpires that we have to know the coefficients cj in order to calculate the dipole moment p. It has turned out that it is not so useful to solve first eqs. (1.13) and (1.14) and then to determine the dipole moment according to (1.19). Rather it has turned out to be preferable to proceed along lines which we have for instance when deriving the Bloch equations of spins. There we have seen that we may obtain equations for the expectation values of the spin components directly and in a very simple fashion. We shall follow the same procedure here, i.e. we wish to derive equations for the expectation value of the dipole moment p. We note that the dipole moment p is known if we know the quantities
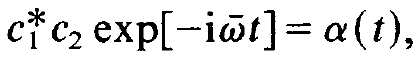 (1.22)
(1.22)
because with their help we may write the dipole moment in the form
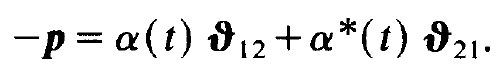 (1.23)
(1.23)
For later purposes we introduce the abbreviations
 (1.24)
(1.24)
so that the dipole moment of the atoms under consideration can be represented in the form
 (1.25)
(1.25)
We now wish to derive an equation for (1.22). The reader will be well advised if he considers α (t) as a measure for the dipole moment of the atoms, i.e. that he connects with the letter a the meaning of a dipole moment. When we differentiate (1.22) with respect to time we obtain
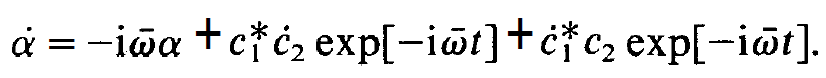 (1.26)
(1.26)
We wish to replace the temporal derivatives of c2 and c1 by means of the r.h.s. of eqs. (1.13) and (1.14) and their complex conjugates, respectively. To this end we write those equations down in a somewhat different shape
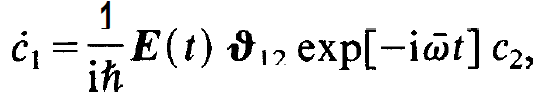 (1.27)
(1.27)
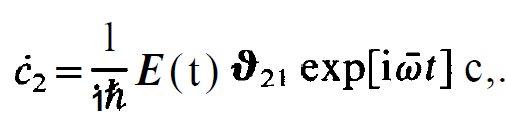 (1.28)
(1.28)
We then obtain for (1.26)
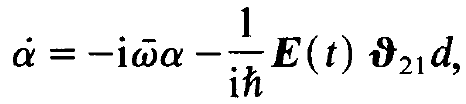 (1.29)
(1.29)
where we have introduced the abbreviation
 (1.30)
(1.30)
It is well known that |cj|2 represents the probability of finding an electron in state j. Equally well, |cj|2 can be considered as the occupation number of state j. Thus (1.30) is a quantum mechanical expression for the occupation number difference or, in other words, for the inversion. In order to make understandable what follows we remind the reader once again of the Bloch equations of spin. The electron of the atom is not only subjected to the external light field but to other perturbations also. For instance in a gas the atom can collide with other atoms all the time. In a solid the electron can interact with lattice vibrations, etc. As we know, such effects cause a damping of the dipole moments. We introduce these dam pings into the theory in a phenomenological manner by adding the damping term - yα to the r.h.s. of eq. (1.29). The damping constant y has the same meaning as the inverse of the transverse relaxation time T2 of a spin. Thus we find for the atom under consideration the equation
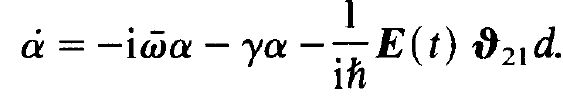 (1.31)
(1.31)
Evidently we have been forced to introduce a new unknown variable namely the inversion (1.30). In order to complete the equations of motion we must derive an equation for the inversion. To this end we differentiate (1.30) with respect to time
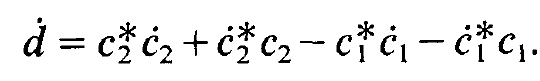 (1.32)
(1.32)
When we replace on its r.h.s. the time derivatives of cj according to the relations (1.27) and (1.28) we obtain after a short transformation
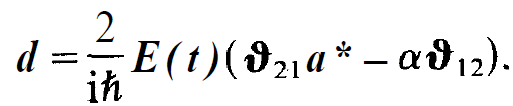 (1.33)
(1.33)
This equation describes how the inversion is changed due to the interaction of the electron and the electric field. When we wish to treat laser processes we must not ignore the interaction of the atom with its surrounding, for instance, we have to pump the atom energetically by a pump process. On the other hand the electron may recombine on account of its interaction with its surrounding. For instance, these processes can consist of radiationless transitions. But we also have to take into account transitions in which light is spontaneously emitted without participating at the proper laser process. All these processes taken together will lead to a relaxation of the inversion towards a stationary value d0 within a characteristic relaxation time T. This effect can be taken care of by adding the corresponding relaxation term to (1.33) so that we obtain
 (1.34)
(1.34)
The time constant T occurring in this equation corresponds to the longitudinal relaxation time T1 of the Bloch theory of spins. Now we have prepared all ingredients in order to formulate the semi classical laser equations but we have to remind ourselves that we are not dealing with a single atom but with an ensemble of N atoms in the laser. For each of these atoms we have derived equations for their "dipole moments" a and inversions d. We remind the reader that α (t) is a dimensionless quantity which is proportional to the dipole moment, however. To underline the physical significance of a we shall call it a dipole moment here and in the following. In order to treat the ensemble of atoms we attach the atomic index p to the corresponding atomic quantities in the equations (1.31)-(1.34).Further more we take into account that the electric field strength E is a function of the atomic positions xμ. Thus we obtain the fundamental matter equations of the laser
 (1.35)
(1.35)
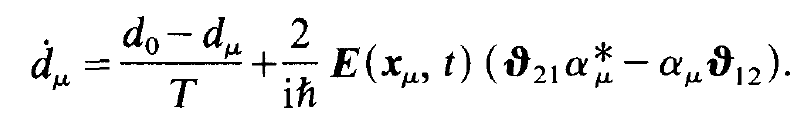 (1.36)
(1.36)
Finally we have to devise a prescription how the macroscopic polarization is connected with the individual dipole moments. To this end we use a mathematical trick by which we write the polarization in the form
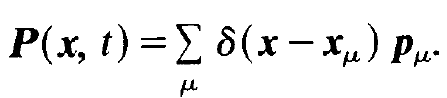 (1.37)
(1.37)
In it δ is Dirac's δ-function which can be visualized as having a peak at point x = xμ and which vanishes otherwise. The sum runs over all the atoms of the material. When we change the coordinate x we palpate the material by means of the &function and each time when an atomic position xμ is hit the corresponding dipole moment p prevails (compare exercise 1). The individual dipole moments pμ are connected with the quantities a, by
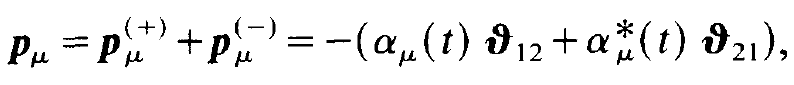 (1.38)
(1.38)
which we have got to know above. Thus we have found a closed system of equations. They consist of the equations for the electric field and of the matter equations (1.35) and (1.36). They are connected in particular by the polarization P according to (1.37) and (1.38). In the following we will transform these equations so that they are more suited for the treatment of the corresponding physical problems.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
خدمات متعددة يقدمها قسم الشؤون الخدمية للزائرين
|
|
|