


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 23-2-2017
Date: 27-2-2017
Date: 18-6-2019
|
Spin and orbital contributions to the magnetic moment
By no means do all paramagnetic complexes obey the spinonly formula and caution must be exercised in its use. It is often the case that moments arising from both the spin and orbital angular momenta contribute to the observed magnetic moment. Details of the Russell–Saunders coupling scheme to obtain the total angular momentum quantum number, J, from quantum numbers L and S are given in Box 20.6, along with notation for state symbols (2S+1)LJ . The energy difference between adjacent states with J values of J’ and (J‘+1) is given by the expression (J’+1)λ where λ is called the spin–orbit coupling constant. For the d2 configuration, for example, the 3F state in an octahedral field is split into states 3F2, 3F3 and 3F4, the energy differences between successive pairs being 3λ and 4λ respectively. In a magnetic field, each state with a different J value splits again to give (2J + 1) different levels separated by gJμBB0 where gJ is a constant called the Lande splitting factor and B0 is the magnetic field; it is the very small energy differences between these levels with which ESR (also called electron paramagnetic resonance, EPR) spectroscopy is concerned. The overall splitting pattern for a d2 ion is shown in Figure 1.1.
The value of λ varies from a fraction of a cm-1 for the very lightest atoms to a few thousand cm-1 for the heaviest ones.
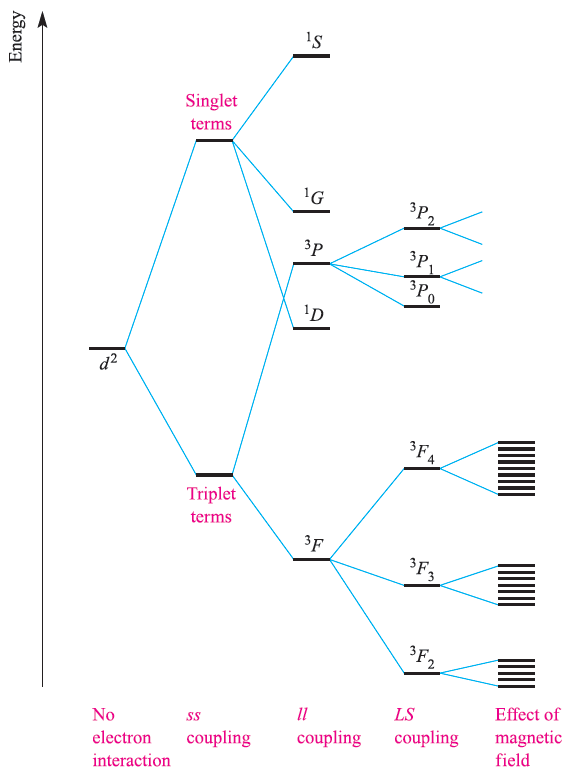
Fig. 1.1 Splitting of the terms of a d2 ion (not to scale).
The extent to which states of different J values are populated at ambient temperature depends on how large their separation is compared with the thermal energy available, kT; at 300 K, kT ≈ 200 cm-1 or 2.6 kJ mol-1. It can be shown theoretically that if the separation of energy levels is large, the magnetic moment is given by equation 1.1. Strictly, this applies only to free-ion energy levels, but it gives values for the magnetic moments of lanthanoid ions (for which λ is typically 1000 cm-1) that are in good agreement with observed values.
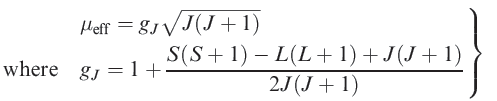 (1.1)
(1.1)
For d-block metal ions, equation 1.1 gives results that correlate poorly with experimental data (Tables 1.1 and ). For many (but not all) first row metal ions, λ is very small and the spin and orbital angular momenta of the electrons operate independently. For this case, the van Vleck formula (equation ) has been derived; strictly, equation applies to free ions but, in a complex ion, the crystal field partly or fully quenches the orbital angular momentum. Data in Tables 1.1 and reveal a poor fit between observed values of μeff and those calculated from equation .
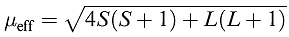 (1.2)
(1.2)
If there is no contribution from orbital motion, then equation reduces to equation 1.3 which is the spin-only formula we met earlier. Any ion for which L = 0 (e.g. high-spin d5 Mn2+ or Fe3+ in which each orbital with ml = 2, 1, 0, _1, _2 is singly occupied, giving L = 0) should, therefore, obey equation 1.3.
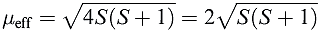 (1.3)
(1.3)
However, some other complex ions also obey the spin-only formula (Tables 1.1 and ). In order for an electron to have orbital angular momentum, it must be possible to transform the orbital it occupies into an entirely equivalent and degenerate orbital by rotation. The electron is then effectively rotating about the axis used for the rotation of the orbital. In an octahedral complex, for example, the three t2g orbitals can be interconverted by rotations through 900; thus, an electron in a t2g orbital has orbital angular momentum. The eg orbitals, having different shapes, cannot be interconverted and so electrons in eg orbitals never have angular momentum. There is, however, another factor that needs to be taken into account: if all the t2g orbitals are singly occupied, an electron in, say, the dxz orbital cannot be transferred into the dxy or dyz orbital because these already contain an electron having the same spin quantum number as the incoming electron. If all the t2g orbitals are doubly occupied, electron transfer is also impossible. It follows that in high-spin octahedral complexes, orbital contributions to the magnetic moment are important only for the configurations t2g1, t2g2, t2g4eg2 and t2g5eg2. For tetrahedral complexes, it is similarly shown that the configurations that give rise to an orbital contribution are e2t21, e2t22, e4t24 and e4t25.
Table Calculated magnetic moments for first row d-block metal ions in high-spin complexes at ambient
temperatures.
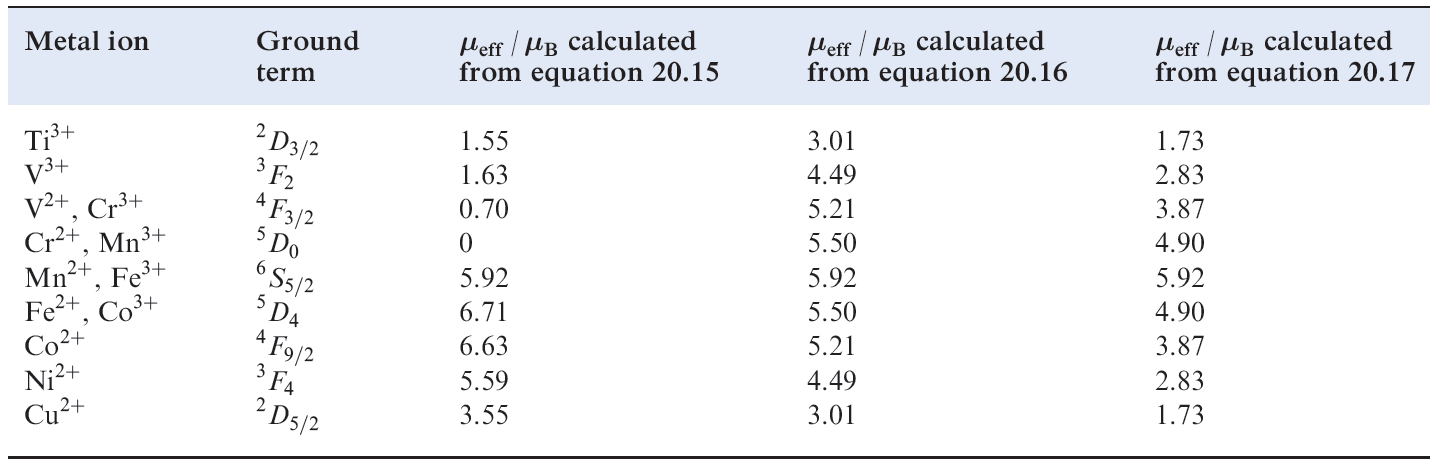
These results lead us to the conclusion that an octahedral high-spin d7 complex should have a magnetic moment greater than the spin-only value of 3.87 μB but a tetrahedral d7 complex should not. However, the observed values of μeff for [Co)H2O(6]2+ and [CoCl4]2- are 5.0 and 4.4 μB respectively, i.e. both complexes have magnetic moments greater than μ (spin-only). The third factor involved is spin–orbit coupling. Spin–orbit coupling is a complicated subject and we can give only a brief mention here; for further details of spin– orbit coupling, see the advanced texts listed in the end-ofchapter reading list. As a result of a mixing of states (which we have so far ignored), theory brings us to equation 1.4; this modifies the μ(spin-only) formula to take into account spin–orbit coupling and, although dependent on Δoct, applies also to tetrahedral complexes.
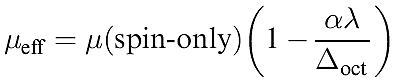 (1.4)
(1.4)
where λ = spin–orbit coupling constant and α = constant that depends on the ground term: α = 4 for an A ground state, and α = 2 for an E ground state. The simple approach of equation 1.4 is not applicable to ions with a T ground state. Some values of λ are given in Table 1.2.
Table 1.2 Spin–orbit coupling coefficients, λ , for selected first row d-block metal ions.

Note that λ is positive for less than half-filled shells and negative for shells that are more than half-filled. Thus, spin–orbit coupling leads to:
An important point is that spin–orbit coupling is generally large for second and third row d-block metal ions and this leads to large discrepancies between μ(spin-only) and observed values of μeff. The d1 complexes cis-[NbBr4(NCMe)2] and cis- [TaCl4(NCMe)2] illustrate this clearly: room temperature values of μeff are 7 and 0.45 μB respectively compared with μ(spin-only) = 1.73μB.


|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|