EXAMPLE 1: DISTANCE BETWEEN TWO SETS. As a first and simple example, let

for A = S¹, the unit sphere in R²: a ∈ S¹ if and only if |a|² = a²₁ +a²₂ = 1. In other words, we are considering only curves that move with unit speed.

We take

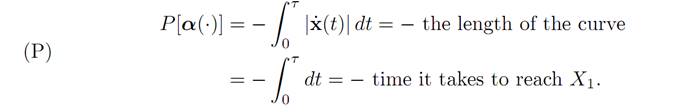
We want to minimize the length of the curve and, as a check on our general theory, will prove that the minimum is of course a straight line.

Using the maximum principle. We have

H(x, p, a) = f (x, a)  p + r(x, a)

                 = a . p − 1 = p₁a₁ + p₂a₂ − 1.

The adjoint dynamics equation (ADJ) says

                                     p˙ (t) = −∇_xH(x(t), p(t),α(t)) = 0,

and therefore

p(t) ≡ constant = p⁰= 0.

The maximization principle (M) tells us that

The right hand side is maximized by

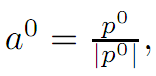
a unit vector that points in the same

direction of p⁰. Thus α(.) ≡ a⁰ is constant in time. According then to (ODE) we have x˙ = a⁰, and consequently x(.) is a straight line.

Finally, the transversality conditions say that

(T)                           p(0) ⊥ T₀, p(t₁) ⊥ T₁.

In other words, p⁰ ⊥ T₀ and p⁰ ⊥ T¹; and this means that the tangent planes T₀ and T₁ are parallel.

Now all of this is pretty obvious from the picture, but it is reassuring that the general theory predicts the proper answer.

 EXAMPLE 2: COMMODITY TRADING. Next is a simple model for the trading of a commodity, say wheat. We let T be the fixed length of trading period, and introduce the variables

x¹ (t) = money on hand at time t

x² (t) = amount of wheat owned at time t

α(t) = rate of buying or selling of wheat

q(t) = price of wheat at time t (known)

          λ = cost of storing a unit amount of wheat for a unit of time.

We suppose that the price of wheat q(t) is known for the entire trading period 0 ≤ t ≤ T (although this is probably unrealistic in practice). We assume also that the rate of selling and buying is constrained:

                                        |α(t)| ≤ M,

where α(t) > 0 means buying wheat, and α(t) < 0 means selling.

Our intention is to maximize our holdings at the end time T, namely the sum of the cash on hand and the value of the wheat we then own:

(P) P[α(.)] = x¹ (T) + q(T)x² (T).

The evolution is

This is a nonautonomous (= time dependent) case, but it turns out that the Pontryagin Maximum Principle still applies.

Using the maximum principle. What is our optimal buying and selling strategy? First, we compute the Hamiltonian

             H(x, p, t, a) = f. p + r = p₁(−λx₂ − q(t)a) + p₂a,

since r ≡ 0. The adjoint dynamics read

with the terminal condition

(T)                                                              p(T) = ∇g(x(T)).

In our case g(x₁, x₂) = x₁ + q(T)x₂, and hence

We then can solve for the costate:

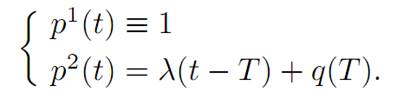
The maximization principle (M) tells us that

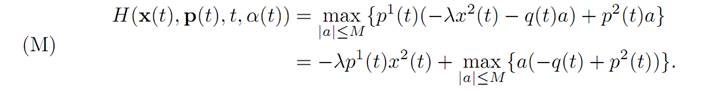
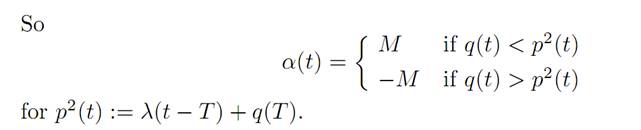
CRITIQUE. In some situations the amount of money on hand x¹(.) becomes negative for part of the time. The economic problem has a natural constraint x₂ ≥ 0  (unless we can borrow with no interest charges) which we did not take into account in the mathematical model.

References

[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.

[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.

[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.

[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.

[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.

[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.

[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.

[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.

[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.

[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).

[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.

[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.

[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.

[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.

[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.

[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.

[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.

[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.

[T] William J. Terrell, Some fundamental control theory I: Controllability, observability,  and duality, American Math Monthly 106 (1999), 705–719.