Let X be a topological space, and let A be a subset of X. A collection of subsets of X in X is said to cover A if and only if every point of A belongs to at least one of these subsets. In particular, an open cover of X is collection of open sets in X that covers X.

If U and V are open covers of some topological space X then V is said to be a subcover of U if and only if every open set belonging to V also belongs to U.

Definition: A topological space X is said to be compact if and only if every open cover of X possesses a finite subcover.

Lemma 1.1 Let X be a topological space. A subset A of X is compact (with respect to the subspace topology on A) if and only if, given any collection U of open sets in X covering A, there exists a finite collection V₁, V₂, . . . , V_r of open sets belonging to U such that A ⊂ V₁ ∪ V₂ ∪ · · · ∪ V_r.

Proof A subset B of A is open in A (with respect to the subspace topology on A) if and only if B = A ∩V for some open set V in X. The desired result therefore follows directly from the definition of compactness.

We now show that any closed bounded interval in the real line is compact.

This result is known as the Heine-Borel Theorem. The proof of this theorem uses the least upper bound principle which states that, given any non-empty set S of real numbers which is bounded above, there exists a least upper bound (or supremum) sup S for the set S.

Theorem 1.2 (Heine-Borel) Let a and b be real numbers satisfying a < b.

Then the closed bounded interval [a, b] is a compact subset of R.

Proof Let U be a collection of open sets in R with the property that each point of the interval [a, b] belongs to at least one of these open sets. We must show that [a, b] is covered by finitely many of these open sets.

Let S be the set of all τ ∈ [a, b] with the property that [a, τ ] is covered by some finite collection of open sets belonging to U, and let s = sup S. Now s ∈ W for some open set W belonging to U. Moreover W is open in R, and therefore there exists some δ > 0 such that (s − δ, s + δ) ⊂ W. Moreover s − δ is not an upper bound for the set S, hence there exists some τ ∈ S satisfying τ > s − δ. It follows from the definition of S that [a, τ ] is covered by some finite collection V₁, V₂, . . . , V_r of open sets belonging to U.

Let t ∈ [a, b] satisfy τ ≤ t < s + δ. Then

                      [a, t] ⊂ [a, τ ] ∪ (s − δ, s + δ) ⊂ V₁ ∪ V₂ ∪ · · · ∪ V_r ∪ W,

and thus t ∈ S. In particular s ∈ S, and moreover s = b, since otherwise s would not be an upper bound of the set S. Thus b ∈ S, and therefore [a, b]  is covered by a finite collection of open sets belonging to U, as required.

Lemma 1.3 Let A be a closed subset of some compact topological space X.

Then A is compact.

Proof Let U be any collection of open sets in X covering A. On adjoining the open set X A to U, we obtain an open cover of X. This open cover of X possesses a finite subcover, since X is compact. Moreover A is covered by the open sets in the collection U that belong to this finite subcover. It follows from Lemma 1.11 that A is compact, as required.

Lemma 1.4 Let f: X → Y be a continuous function between topological spaces X and Y , and let A be a compact subset of X. Then f(A) is a compact subset of Y .

Proof Let V be a collection of open sets in Y which covers f(A). Then A is covered by the collection of all open sets of the form f⁻¹ (V ) for some V ∈ V.

It follows from the compactness of A that there exists a finite collection V₁, V₂, . . . , V_k of open sets belonging to V such that A ⊂ f⁻¹ (V₁) ∪ f⁻¹ (V₂) ∪ · · · ∪ f⁻¹ (Vk).

But then f(A) ⊂ V₁ ∪ V₂ ∪ · · · ∪ V_k. This shows that f(A) is compact.

Lemma 1.5 Let f:X → R be a continuous real-valued function on a compact topological space X. Then f is bounded above and below on X.

Proof  The range f(X) of the function f is covered by some finite collection I₁, I₂, . . . , I_k of open intervals of the form (−m, m), where m ∈ N, since f(X)  is compact (Lemma 1.14) and R is covered by the collection of all intervals of this form. It follows that f(X) ⊂ (−M, M), where (−M, M) is the largest of the intervals I₁, I₂, . . . , I_k. Thus the function f is bounded above and below on X, as required.

Proposition 1.6 Let f: X → R be a continuous real-valued function on a compact topological space X. Then there exist points u and v of X such that f(u) ≤ f(x) ≤ f(v) for all x ∈ X.

Proof Let m = inf{f(x) : x ∈ X} and M = sup{f(x) : x ∈ X}. There must exist v ∈ X satisfying f(v) = M, for if f(x) < M for all x ∈ X then the function x → 1/(M − f(x)) would be a continuous real-valued function on X that was not bounded above, contradicting Lemma 1.15. Similarly there must exist u ∈ X satisfying f(u) = m, since otherwise the function    x → 1/(f(x)−m) would be a continuous function on X that was not bounded above, again contradicting Lemma 1.15. But then f(u) ≤ f(x) ≤ f(v) for all x ∈ X, as required.

Proposition 1.7 Let A be a compact subset of a metric space X. Then A is closed in X.

Proof Let p be a point of X that does not belong to A, and let f(x) = d(x,p), where d is the distance function on X. It follows from Proposition 1.16 that there is a point q of A such that f(a) ≥ f(q) for all a ∈ A,  since A is compact. Now f(q) > 0, since q ≠p. Let δ satisfy 0 < δ ≤ f(q).

Then the open ball of radius about the point p is contained in the complement of δ, since f(x) < f(q) for all points x of this open ball. It follows that the complement of A is an open set in X, and thus A itself is closed in X.

Proposition 1.8 Let X be a Hausdorff topological space, and let K be a compact subset of X. Let x be a point of X K. Then there exist open sets V and W in X such that x ∈ V , K ⊂ W and V ∩ W = ∅.

Proof For each point y ∈ K there exist open sets V_x,y and W_x,y such that x ∈ V_x,y, y ∈ W_x,y and V_x,y ∩ W_x,y = ∅ (since X is a Hausdorff space). But then there exists a finite set {y₁, y₂, . . . , y_r} of points of K such that K is contained in W_x,y1 ∪ W_x,y2 ∪ · · · ∪ _Wx,yr, since K is compact. Define

                                  V = V_x,y1 ∩ V_x,y2 ∩ · · · ∩ V_x,yr , W = W_x,y1 ∪ W_x,y2 ∪ · · · ∪ W_x,yr.

Then V and W are open sets, x ∈ V , K ⊂ W and V ∩W = ∅, as required.

Corollary 1.9 A compact subset of a Hausdorff topological space is closed.

Proof Let K be a compact subset of a Hausdorff topological space X. It follows immediately from Proposition 1.18 that, for each x ∈ X K, there exists an open set V_x such that      x ∈ V_x and V_x ∩ K = ∅. But then X K is equal to the union of the open sets Vx as x ranges over all points of X K, and any set that is a union of open sets is itself an open set. We conclude that X K is open, and thus K is closed.

Proposition 1.10 Let X be a Hausdorff topological space, and let K₁ and K₂ be compact subsets of X, where K₁ ∩ K₂ = ∅. Then there exist open sets U₁ and U₂ such that K₁ ⊂ U₁, K₂ ⊂ U₂ and U₁ ∩ U₂ = ∅.

Proof It follows from Proposition 1.18 that, for each point x of K₁, there exist open sets V_x and W_x such that x ∈ V_x, K₂ ⊂ W_x and V_x ∩W_x = ∅. But then there exists a finite set {x₁, x₂, . . . , x_r} of points of K1 such that

                                K₁ ⊂ V_x1 ∪ V_x2 ∪ · · · ∪ V_xr,

since K₁ is compact. DefineU₁ = V_x1 ∪ V_x2 ∪ · · · ∪ V_xr, U₂ = W_x1 ∩ W_x2 ∩ · · · ∩ W_xr.

Then U₁ and U₂ are open sets, K₁ ⊂ U₁, K₂ ⊂ U₂ and U₁ ∩ U₂ = ∅, as required.

Lemma 1.11 Let f:X → Y be a continuous function from a compact topological space X to a Hausdorff space Y . Then f(K) is closed in Y for every closed set K in X.

Proof If K is a closed set in X, then K is compact (Lemma 1.13), and therefore f(K) is compact (Lemma 1.14). But any compact subset of a Hausdorff space is closed (Corollary 1.19). Thus f(K) is closed in Y , as required.

Remark : If the Hausdorff space Y in Lemma 1.21 is a metric space, then Proposition 1.17 may be used in place of Corollary 1.12 in the proof of the lemma.

Theorem 1.13 A continuous bijection f: X → Y from a compact topological space X to a Hausdorff space Y is a homeomorphism.

Proof Let g: Y → X be the inverse of the bijection f: X → Y . If U is open in X then X U is closed in X, and hence f(X U) is closed in Y ,  by Lemma 1.21. But f(X U) = g⁻¹ (X U) = Y g⁻¹ (U). It follows that g⁻¹ (U) is open in Y for every open set U in X. Therefore g: Y → X is continuous, and thus f: X → Y is a homeomorphism.

We recall that a function f: X → Y from a topological space X to a topological space Y is said to be an identification map if it is surjective and satisfies the following condition: a subset U of Y is open in Y if and only if f⁻¹ (U) is open in X.

Proposition 1.14 A continuous surjection f:X ! Y from a compact topological space X to a Hausdorff  space Y is an identication map.

Proof Let U be a subset of Y . We claim that Y U = f(K), where K =X f⁻¹ (U). Clearly f(K) ⊂ Y U. Also, given any y ∈ Y U, there exists x ∈ X satisfying y = f(x), since f: X → Y is surjective. Moreover x ∈ K, since f(x) ∉U. Thus Y U ⊂ f(K), and hence Y U = f(K), as claimed.

We must show that the set U is open in Y if and only if f⁻¹ (U) is open in X. First suppose that f⁻¹ (U) is open in X. Then K is closed in X, andhence f(K) is closed in Y , by Lemma 1.21. It follows that U is open in Y .

Conversely if U is open in Y then f⁻¹ (U) is open in X, since f: X → Y is continuous. Thus the surjection f: X → Y is an identification map.

Example Let S¹ be the unit circle in R², defined by S¹ = {(x, y) ∈ R²: x² + y² = 1}, and let q: [0, 1] → S¹ be defined by q(t) = (cos 2πt,sin 2πt) for all t ∈ [0, 1]. It has been shown that the map q is an identification map. This also follows directly from the fact that q: [0, 1] → S¹is a continuoussurjection from the compact space [0, 1] to the Hausdorff space S¹.

We shall show that a finite Cartesian product of compact spaces is compact. To prove this, we apply the following result, known as the Tube Lemma.

Lemma 1.15 Let X and Y be topological spaces, let K be a compact subset of Y , and U be an open set in X × Y . Let V = {x ∈ X : {x} × K ⊂ U}.

Then V is an open set in X.

Proof Let x ∈ V . For each y ∈ K there exist open subsets D_y and E_y of X and Y respectively such that (x, y) ∈ D_y × E_y and D_y × E_y ⊂ U.

Now there exists a finite set {y₁, y₂, . . . , y_k} of points of K such that K ⊂ Ey₁ ∪ Ey₂ ∪ · · · ∪ E_yk, since K is compact. Set N_x = D_y1 ∩ D_y2 ∩ · · · ∩ D_yk.

Then N_x is an open set in X. Moreover

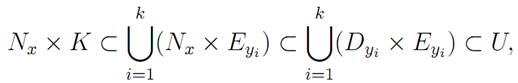
so that N_x ⊂ V . It follows that V is the union of the open sets N_x for all x ∈ V . Thus V is itself an open set in X, as required.

Theorem 1.16 A Cartesian product of a finite number of compact spaces is itself compact.

Proof It suffices to prove that the product of two compact topological spaces X and Y is compact, since the general result then follows easily by induction on the number of compact spaces in the product.

Let U be an open cover of X × Y . We must show that this open cover possesses a finite subcover.

Let x be a point of X. The set {x}×Y is a compact subset of X ×Y , since it is the image of the compact space Y under the continuous map from Y to X × Y which sends y ∈ Y to (x, y), and the image of any compact set under a continuous map is itself compact (Lemma 1.14). Therefore there exists a finite collection U₁, U₂, . . . , U_r of open sets belonging to the open cover U such that {x} × Y is contained in U₁ ∪ U₂ ∪ · · · ∪U_r. Let Vx denote the set of all points x₀ of X for which {x₀} × Y is contained in U₁ ∪ U₂ ∪ · · · ∪U_r. Then x ∈ V_x, and

Lemma 1.17 ensures That V_x is an open set in X. Note that V_x × Y is covered by finitely many of the open sets belonging to the open cover U.

Now {V_x : x ∈ X} is an open cover of the space X. It follows from the compactness of X that there exists a finite set {x₁, x₂, . . . , x_r} of points of X such that X = Vx₁ ∪ Vx₂ ∪ · · · ∪ Vx_r. Now X × Y is the union of the sets V_xj × Y for j = 1, 2, . . . , r, and each of these sets can be covered by a finite collection of open sets belonging to the open cover U. On combining these finite collections, we obtain a finite collection of open sets belonging to U which covers X × Y . This shows that X × Y is compact.

Theorem 1.18 Let K be a subset of Rⁿ. Then K is compact if and only if K is both closed and bounded.

Proof Suppose that K is compact. Then K is closed, since Rn is Hausdorff, and a compact subset of a Hausdorff space is closed (by Corollary 1.19). For each natural number m, let Bm be the open ball of radius m about the origin,  given by B_m = {x ∈ Rⁿ: |x| < m}. Then {B_m : m ∈ N} is an open cover of Rⁿ. It follows from the compactness of K that there exist natural numbers  m₁, m₂, . . . , m_k such that K ⊂ B_m1 ∪ B_m2 ∪ · · · ∪ B_mk . But then K ⊂ B_M,  where M is the maximum of m₁, m₂, . . . , m_k, and thus K is bounded.

Conversely suppose that K is both closed and bounded. Then there exists some real number L such that K is contained within the closed cube C given by

        C = {(x₁, x₂, . . . , x_n) ∈ Rⁿ : −L ≤ x_j ≤ L for j = 1, 2, . . . , n}.