
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Nuclear Magnetic Resonance
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 63
19-8-2016
1767
Nuclear Magnetic Resonance
A spin-1/2 nucleus is placed in a large magnetic field B0 in the z-direction. An oscillating field B1 << B0 of radio frequency is applied in the xy-plane, so the total magnetic field is
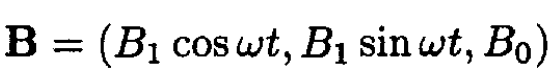 (1)
(1)
The Hamiltonian is H = μB . σ, where μ is the magnetic moment. Use the notation hΩ|| = μB0, hΩ┴ = μB1.
a) If the nucleus is initially pointing in the +z-direction at t = 0, what is the probability that it points in the -z-direction at later times?
b) Discuss why most NMR experiments adjust B0 so that Ω|| ~ ω/2.
SOLUTION
a) Let and denote the probability of spin up and spin down as a function of time. The time-dependent Hamiltonian is
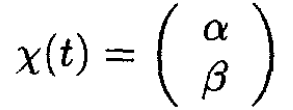 (1)
(1)
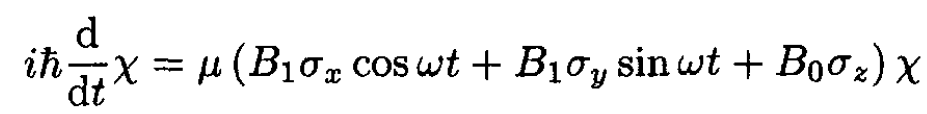 (2)
(2)
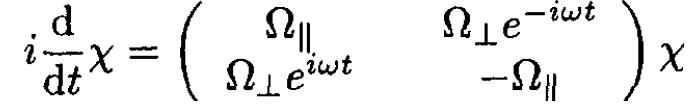 (3)
(3)
The equations for the individual components are
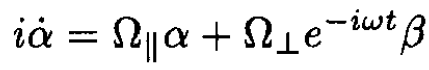 (4)
(4)
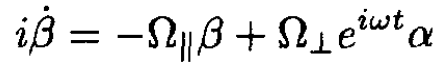 (5)
(5)
where the overdots denote time derivatives. We solve the first equation for β and substitute this into the second equation:
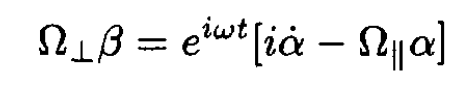 (6)
(6)
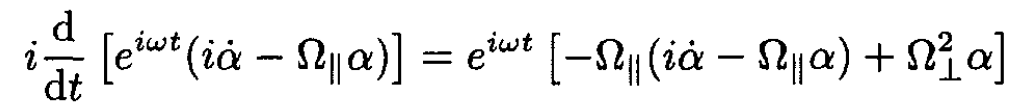 (7)
(7)
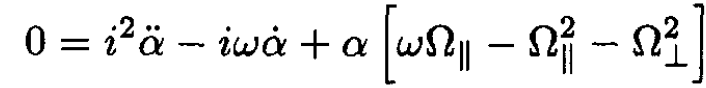 (8)
(8)
We assume that
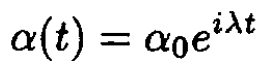 (9)
(9)
We determine the eigenvalue frequency λ by inserting the above form for α(t) into (8), which gives a quadratic equation for that has two roots:
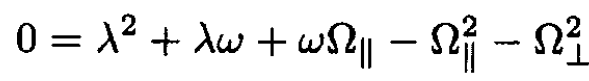 (10)
(10)
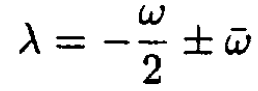 (11)
(11)
 (12)
(12)
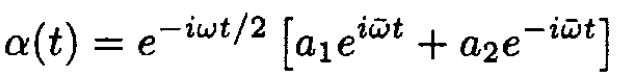 (13)
(13)
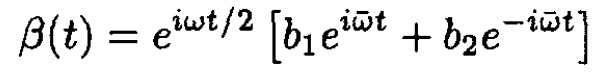 (14)
(14)
We have introduced the constants a1, a2, b1, b2. They are not all independent. Inserting these forms into the original differential equations, we obtain two relations which can be used to give
 (15)
(15)
 (16)
(16)
This completes the most general solution. Now we apply the initial conditions that the spin was pointing along the z-axis at t = 0. This gives α(0) = 1, which makes a1 + a2 = 1, and β(0) = 0, which gives b1 + b2 = 0. These two conditions are sufficient to find
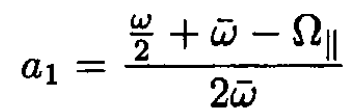 (17)
(17)
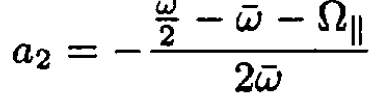 (18)
(18)
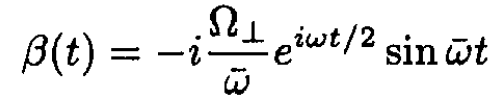 (19)
(19)
 (20)
(20)
The probability of spin up is |α(t)|2 and that of spin down is |β(t)|2:
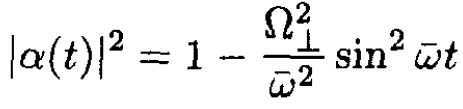 (21)
(21)
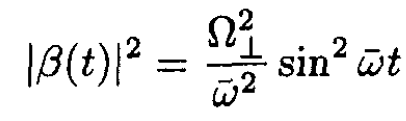 (22)
(22)
b) In the usual NMR experiment, one chooses the field B0 so that 2Ω|| ≈ ω, in which case  and
and and
and 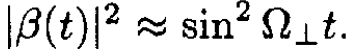 The spin oscillates slowly between the up and down states.
The spin oscillates slowly between the up and down states.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















