


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 28-7-2016
Date: 13-7-2016
Date: 29-8-2016
|
Given Another Eigenfunction
A nonrelativistic particle of mass m moves in a three-dimensional central potential V(r) which vanishes at r → ∞. We are given that an exact eigenstate is
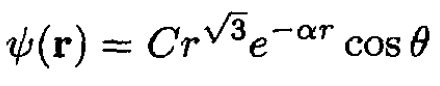 (i)
(i)
where C and α are constants.
a) What is the angular momentum of this state?
b) What is the energy?
c) What is V(r)?
SOLUTION
a) The factor cos θ indicates that it is a pz state which has an angular momentum of 1.
b) In order to determine the energy and potential, we operate on the eigenstate with the kinetic energy operator. For ℓ = 1 this gives for the radial part 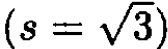
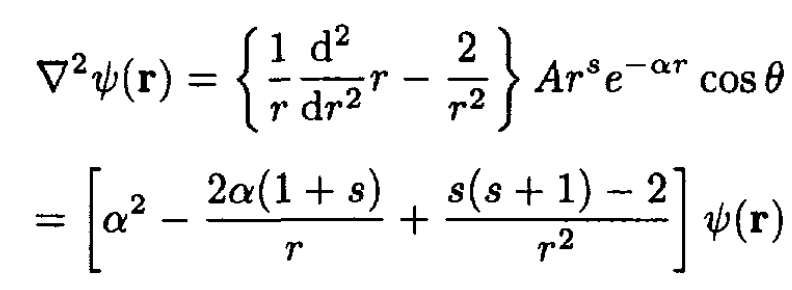 (1)
(1)
The constant in the last term can be simplified to 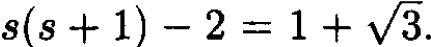 In the limit r → ∞, the potential vanishes, and only the constant term in the kinetic energy equals the eigenvalue. Thus, we find
In the limit r → ∞, the potential vanishes, and only the constant term in the kinetic energy equals the eigenvalue. Thus, we find
 (2)
(2)
c) To find the potential we subtract the kinetic energy from the eigenvalue and act on the eigenfunction:
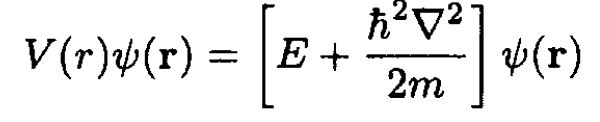 (3)
(3)
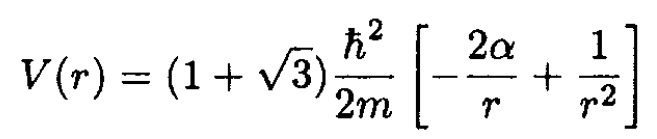 (4)
(4)
The potential has an attractive Coulomb term ~1/r and a repulsive 1/r2 term.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|