Potential above Half Planes

An infinite conducting plane (the x-z plane in Figure 1.1) is divided by the line z = 0. For x > 0, the potential in the plane is +V₀, while for x < 0. the potential is –V₀. Evaluate the potential everywhere.

Figure 1.1

SOLUTION

This problem is symmetric for displacements along the z-axis, so we can consider this a two-dimensional problem in the x – y plane, a candidate for the method of conformal mapping. It can be seen that the function ω = ln η (η = x +iy, ω = u + iv) transforms the initial plane so that points at y = 0 for map into the line v = 0, and the points at y = 0 for x < 0 map into the line v = π (see Figure 1.2). In the plane

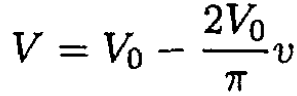
so that at v = 0, V = V₀ and at v = π, V = -V₀. Again using

Figure 1.2

η = x – iy = ρe^iφ, we obtain

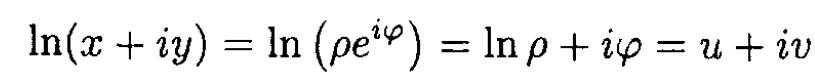
so that

We then have

and

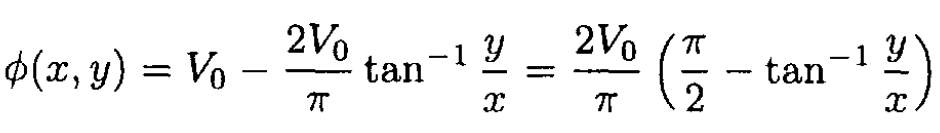
or using

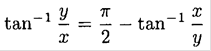
we find

We can check that ϕ (x, y) satisfies the boundary conditions.