
Mass Orbiting on Table
 المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 15
الجزء والصفحة:
part 1 , p 15
 28-7-2016
28-7-2016
 1820
1820
Mass Orbiting on Table
A particle of mass M is constrained to move on a horizontal plane. A second particle, of mass m, is constrained to a vertical line. The two particles are connected by a massless string which passes through a hole in the plane (see Figure 1.1). The motion is frictionless.

Figure 1.1
a) Find the Lagrangian of the system and derive the equations of motion.
b) Show that the orbit is stable with respect to small changes in the radius, and find the frequency of small oscillations.
SOLUTION
a) We can write the Lagrangian in terms of the length r of the string on the table and the angle θ (see Figure 1.2):

The equations of motion are
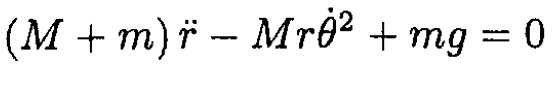 (1)
(1)
 (2)
(2)

Figure 1.2
we have angular momentum conservation: 


b) The equilibrium position is defined by taking the derivative of Ueff where

∂2Ueff/∂r2 > 0, so the orbit is stable with respect to a small perturbation in the radius. The frequency of small oscillations is given by

 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


