Green’s Reciprocation Theorem

a) Prove Green’s reciprocation theorem: If ϕ is the potential due to a volume charge density ρ within a volume V and a surface charge density σ on the conducting surface S bounding the volume V, while ϕ' is the potential due to another charge distribution ρ' and σ' then

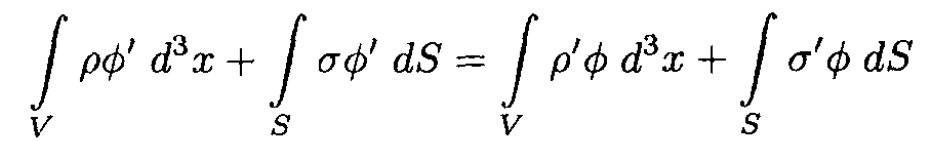
b) A point charge q is placed between two infinite grounded parallel conducting plates. If z₀ is the distance between q and the lower plate, find the total charge induced on the upper plate in terms of q, z₀, and l, where l is the distance between the plates (see Figure 1.1). Show your method clearly.

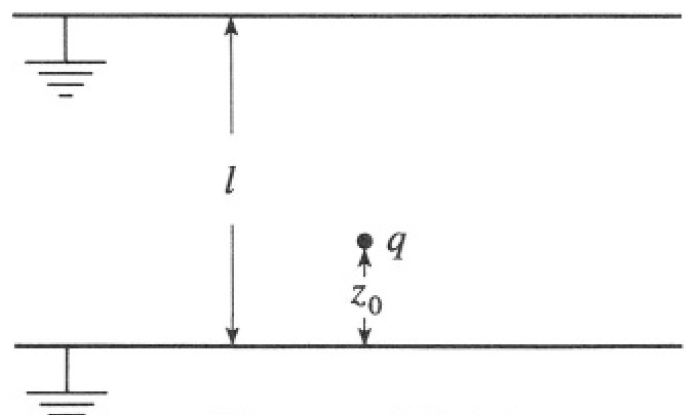
Figure 1.1

SOLUTION

a) We may prove the theorem by considering the volume integral of the following expression:

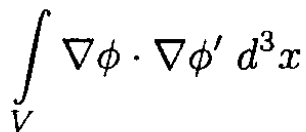
Integrating by parts in two ways, we have

(1)

Now, 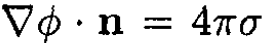 (where n points opposite to the directed area of the surface S) and  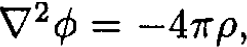so dividing (1) by 4π yields the desired result:

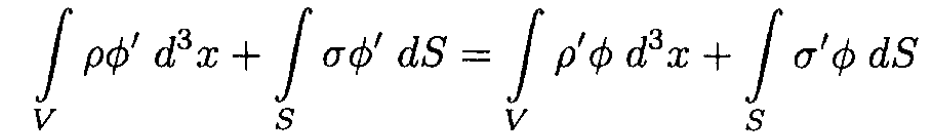(2)

b) Let us introduce a second potential given by ϕ' = 2πσ' z, corresponding to a surface charge density on the upper plate of σ' and on the lower plate of 0 (see Figure 1.2). This introduced potential has no charge in the volume, and the real potential is zero on the plates so that the right-hand side of (2) is zero, yielding

where Q_i is the induced charge. So on the upper plate,

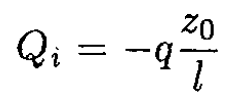
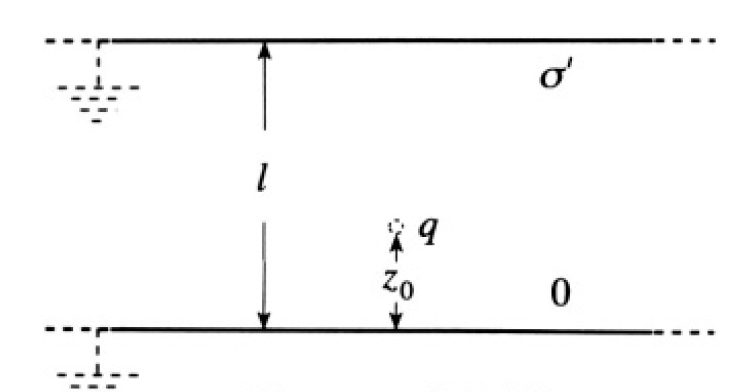
Figure 1.2