We end this section on matchings by discussing perfect matchings. Recall that a perfect matching is a matching that saturates the entire vertex set of a graph.What kinds of graphs have perfect matchings? One thing that is clear is that a graph must be of even order in order to have a chance at having a perfect matching. But being of even order is certainly not enough to guarantee a perfect matching (look back at Figure 1.1).

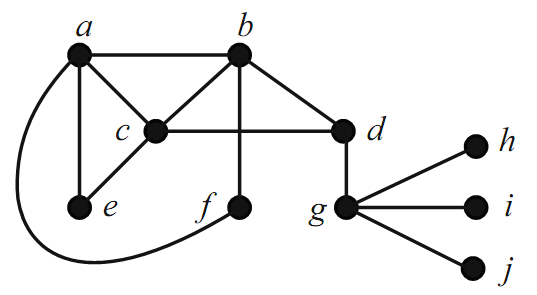
                                            Figure 1.1

We do know that K_2n, C_2n,and P_2n have perfect matchings. The following result regarding perfect matchings in bipartite graphs is a corollary to Hall’s Theorem. The proof is left as an exercise (Exercise 3).

Corollary 1.1.

 If G is a bipartite graph that is regular of degree k, then G contains a perfect matching.

It seems very natural to think that the more edges a graph has, the more likely it is that the graph will have a perfect matching. The following theorem verifies this thought, to a degree.

Theorem 1.1.

If G is a graph of order 2n such that δ(G) ≥ n, then G has a perfect matching.

Proof. Let G be a graph of order 2n with δ(G) ≥ n. Dirac’s theorem (Let G be a graph of order n ≥ 3.If δ(G) ≥ n/2,then G is Hamiltonian.) guarantees the existence of a Hamiltonian cycle, C. A perfect matching of G is formed by using alternate edges of C.

In 1947 Tutte [2] provided perhaps the best known characterization of graphs with perfect matchings. A number of proofs of Tutte’s Theorem have been published since then. The proof that we present is due to Anderson [3]. A definition first: Given a graph G, define Ω(G) to be the number of connected components of G with odd order. Also, define Σ(G) to be the number of connected components of G with even order.

Theorem 1.2 (Tutte’s Theorem).

 Let G be a graph of order n ≥ 2. G has a perfect matching if and only if Ω(G − S) ≤|S| for all subsets of S of V (G).

Proof. We begin with the forward direction. Let G be a graph that has a perfect matching. Suppose S is a set of vertices and that O₁, O₂,... , O_k are the odd components of G−S. For each i, the vertices in O_i can be adjacent only to other vertices in O_i and to vertices in S. Since G has a perfect matching, at least one vertex out of each of the O_i’s has to be matched with a different vertex in S. If k> |S|, then some O_i would be left out (Figure 1.2). Thus, k ≤|S|.

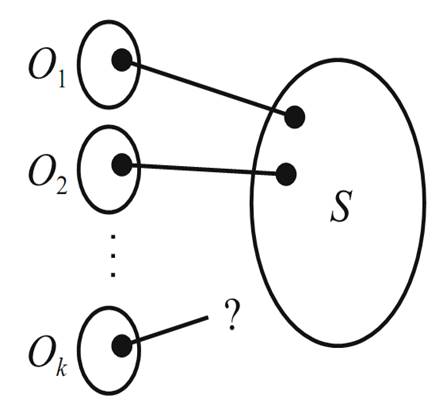
                                       FIGURE 1.2.

For the reverse direction of the theorem, suppose that |S|≥ Ω(G − S) for all S. In particular, if S = ∅,then Ω(G −∅) ≤ 0. This implies that there are no odd components of G—every component of G is even. More generally, we make the following claim.

Claim A. For any proper subset S, |S| and Ω(G − S) are either both even or both odd.

           Let C be some component of G. We know from earlier that C has even order. If an even number of vertices is removed from C, then the number of odd components remaining must also be even. If an odd number of vertices is removed from C, then the number of odd components remaining must be odd. Since this is true for every  component of G, it is true for all of G. Hence Claim A is proved.

We now proceed by induction on n, the order of the graph. If n =2,then G is K₂, which certainly has a perfect matching. Suppose now that the result is true for all graphs of even order up to n, and let G be a graph of even order n. We now have two cases.

Case 1. Suppose that for every proper subset S, Ω(G − S) < |S|.(Thatis, thestrict inequality holds.) Claim A implies that |S| and Ω(G − S) have the same parity, so we can say in this case that for all subsets S, Ω(G − S) ≤|S|− 2.Let uv ∈ E(G), and consider the graph G − u − v (a graph with two fewer vertices than G). We would like to apply the induction hypothesis to G − u − v, so we need the following claim.

Claim B. For all subsets S^/ of V (G − u − v), Ω(G − u − v – S^/) ≤|S^/|.

If Claim B were not true, then Ω(G−u−v−S1) > |S1| for some subset S1.But since |S1| = |S1 ∪{u, v}| − 2,weget Ω(G − u − v − S1) > |S1 ∪{u, v}|,and this contradicts the assumption in this case. Claim B is proved. Since Claim B is true, we can apply the induction hypothesis to G − u − v.

That is, we can conclude that G − u − v has a perfect matching. This matching, together with the edge uv, forms a perfect matching of G. Case 1 is complete.

Case 2. Suppose there exists a subset S such that Ω(G − S)= |S|.There may be a number of subsets S that satisfy this condition—suppose without loss of generality that S is a largest such set. Let O₁, O₂, ... , O_k be the components of G − S of odd order.

Claim C. Σ(G − S)=0. That is, there are no even-ordered components of G − S.

Let E be an even ordered component of G − S,and let x be a vertex of E. The graph G − S − x has exactly one more odd component than G − S. Thus,  |S ∪{x}| =Ω(G − S − x). But this means that S ∪{x} is a set larger than S that satisfies the assumption of this case. Since we chose S to be the largest, we have a contradiction. Therefore there are no even-ordered components of G − S. Claim C is proved. Claim D. There exist vertices s₁, s₂, ... , s_k ∈ S and

vertices v₁, v₂, ... , v_k, where for each iv_i ∈ O_i, such that {v₁s₁,v₂s₂,...,v_ks_k} is a matching.For each i ∈{1,...,k}, define the set Si to be the set of vertices in S that are adjacent to some vertex in O_i. Note that if S_i = ∅ for some i, then O_i is completely disconnected from anything else in G, implying that G itself has an odd component. Since this contradicts our assumption in this case, we can assume that each S_i is nonempty. Furthermore, our initial assumptions imply that the union of any r of the S_i’s has size at least r.  is satisfied, implying that there exists a system of distinct representatives for the family of sets S₁, S₂, ... , S_k. If we let  these representatives be s₁, s₂, ... , s_k, and their adjacencies in the O_i’s be v₁, v₂, ... , v_k, then Claim D is proved.

The situation in G is depicted in Figure 1.3, where k = |S|.

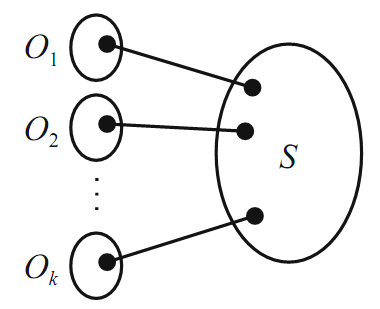
                         FIGURE 1.3.

At this point, each vertex in S has been matched to a vertex in an O_i. The goal at this point is to show that each O_i − v_i has a perfect matching.

Let W be some subset of vertices of (the even-ordered) O_i − v_i.

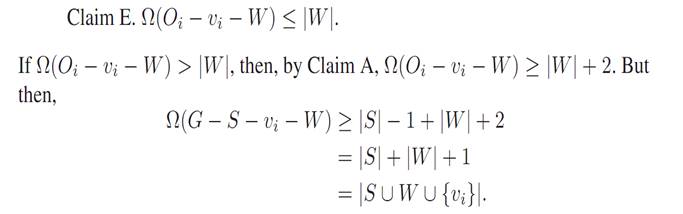
This contradicts our assumption, and thus Claim E is proved. Since Claim E is true, each O_i − v_i satisfies the induction hypothesis, and thus has a perfect matching. These perfect matchings together with the perfect matching shown in Figure 1.3 form a perfect matching of  G, and so Case 2 is complete.

We conclude this section by considering perfect matchings in regular graphs. If a graph G is 1-regular, then G itself is a perfect matching. If G is 2-regular, then G is a collection of disjoint cycles; as long as each cycle is even, G will have a perfect matching.

What about 3-regular graphs? A graph that is 3-regular must be of even order, so is it possible that every 3-regular graph contains a perfect matching? In a word,  no. The graph in Figure 1.4 is a connected 3-regular graph that does not have a perfect matching. Thanks to Petersen [4], though, we do know of a special class of 3-regular graphs that do have perfect matchings. Recall that a bridge in a graph is an edge whose removal would disconnect the graph. The graph in Figure 1.4has three bridges.

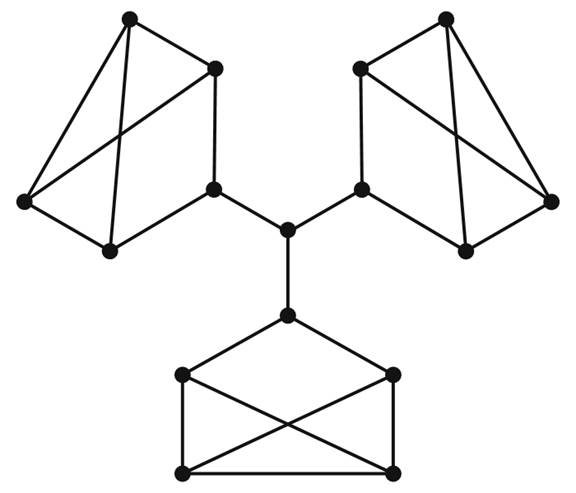
                                                  FIGURE 1.4.

Theorem 1.3 (Petersen’s Theorem).

Every bridgeless, 3-regular graph contains a perfect matching.

Proof. Let G be a bridgeless, 3-regular graph, and suppose that it does not contain a perfect matching. By Tutte’s Theorem, there must exist a subset S of vertices where the number of odd components of G − S is greater than |S|. Denote the odd-ordered components of G − S by O₁, O₂, ... , O_k.

First, each O_i must have at least one edge into S. Otherwise, there would exist an odd-ordered, 3-regular subgraph of G, and this is not possible, by Theorem1.1.

Second, since G is bridgeless, there must be at least two edges joining each O_i to S. Moreover, if there were only two edges joining some O_i to S, then O_i would contain an odd number of vertices with odd degree, and this cannot happen. We can therefore conclude that there are at least three edges joining each O_i to S. This implies that there are at least 3k edges coming into S from the O_i’s. But since every vertex of S has degree 3, the greatest number of edges incident with vertices in S is 3|S|, and since 3k> 3|S|, we have a contradiction. Therefore, G must have a perfect matching.

             It is probably not surprising that the Petersen of Theorem 1.3 is the same person for whom the Petersen graph (Figure 1.5) is named.

Petersen used this special graph as an example of a 3-regular, bridgeless graph whose edges cannot be partitioned into three separate, disjoint matchings.

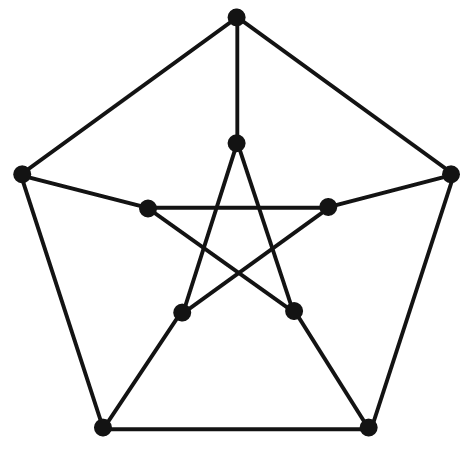
                    FIGURE 1.5 The Petersen Graph.

1-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(111-116)

2- W. T. Tutte, The factorization of linear graphs, J. LondonMath. Soc. 22 (1947), no. 2, 107–111.

3- I. Anderson, Perfect matchings of a graph, J. Combin. Theory Ser. B 10 (1971), no. 3, 183–186.

4-J. Petersen, Die Theorie der regul¨ aren Graphen, Acta Math. 15 (1891), 193–220.