


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-5-2022
Date: 9-2-2016
Date: 4-5-2022
|
The problem of the chromatic index of a simple graph is a remarkable example of an NP-complete problem (even when the NP-completeness has been found much later than for other graph problems). Indeed, deciding if the chromatic index of a simple graph is Δ or Δ + 1 is an NP-complete problem.
Nevertheless, the problem of finding in a simple graph a maximum matching, that is one having the largest number of edges possible, can be solved by a polynomial algorithm. Indeed, it is with this problem that the concept of polynomial complexity was introduced. It is then possible to think of the following algorithm to find the chromatic index of a graph, this index being seen here as the lowest number of classes of a partition of edges into matchings: consider a maximum matching C1 of G, and then a maximum matching C2 of G − C1, the graph obtained by removing the edges of C1, and so on until the removal of all edges of G. The matchings successively obtained, C1,C2,... of G, construct an edge partition into matchings of the graph. We have tried to minimize the number of these matchings by considering each time a matching with a maximum number of edges in what was left. This way of proceeding means giving a first color as often as possible to some edges of the graph, while respecting the condition of never giving the same color to two edges sharing the same end vertex. We then give a second color to a maximum number of edges not yet colored, and so forth until all edges of the graph are colored. Unfortunately, this greedy algorithm (see Chapter of tree) in general does not yield an optimal result, that is, a coloring with the lowest possible number of colors, as shown in Figure 1.1.
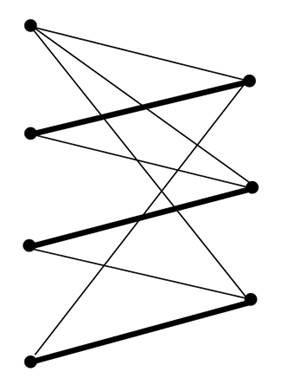
Figure 1.1. By giving a first color to the edges of the maximum matching shown in bold, it will not be possible to have a Δ-coloring of this bipartite graph of maximum degree 3 (because of the degree 3 vertex on the upper left).
Nevertheless such a coloring exists It is always possible to try every way of giving colors to the edges to find a coloring. There is a general classic method called backtracking. It equates to a depth–first search of an arborescence (an algorithm studied in Chapter of Search Algorithms). In fact it is a very good anticipation exercise to try to implement this search for the chromatic index of the graph, called the Petersen graph, shown in Figure 1.2. This graph does not have a Δ-coloring; its chromatic index is not 3 but 4.
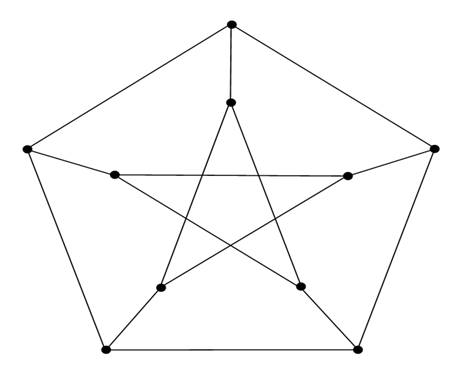
Figure 1.2. Petersen’s graph (chromatic index =4)
In fact, there is no other real general method known at present to verify that there is no Δ-coloring. However, the number of cases increases exponentially with the size of the graph, showing all too well the difficulty of an NP-complete problem.
The case of bipartite graphs is algorithmically more accessible. It is possible to find with a polynomial algorithm a Δ-coloring of any bipartite graph (simple or not). This is particularly interesting in relation to the timetabling problem. The study of such an algorithm is proposed as an exercise at the end of this chapter.
Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(73-75)



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|