


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-10-2016
Date: 3-10-2016
Date: 5-10-2016
|
THE BASIC PROBLEM.
DYNAMICS. We open our discussion by considering an ordinary differential equation (ODE) having the form

We are here given the initial point x0 ∈ Rn and the function f : Rn → Rn. The unknown is the curve x : [0,∞) → Rn, which we interpret as the dynamical evolution of the state of some “system”.
CONTROLLED DYNAMICS. We generalize a bit and suppose now that f depends also upon some “control” parameters belonging to a set A ⊂ Rm; so that f : Rn×A → Rn. Then if we select some value a ∈ A and consider the corresponding dynamics:
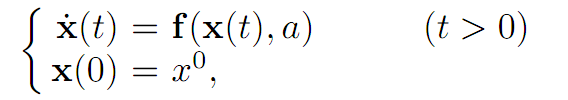
we obtain the evolution of our system when the parameter is constantly set to thevalue a.
The next possibility is that we change the value of the parameter as the system evolves. For instance, suppose we define the function α : [0,∞) → A this way:
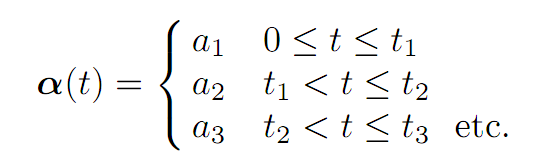
for times 0 < t1 < t2 < t3 . . . and parameter values a1, a2, a3,…..∈ A; and we then solve the dynamical equation

The picture illustrates the resulting evolution. The point is that the system may behave quite differently as we change the control parameters.
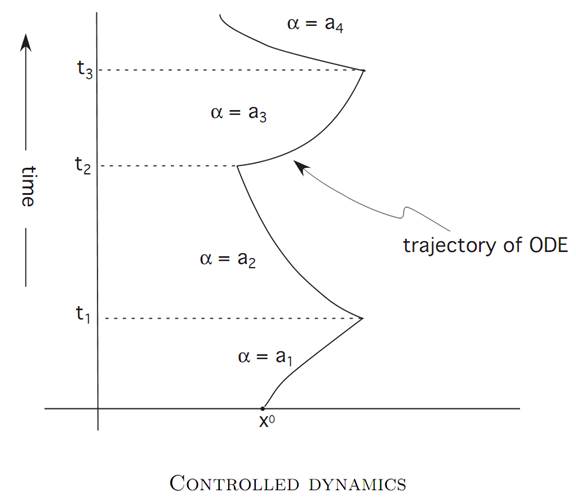
More generally, we call a function α : [0,∞) → A a control. Corresponding to each control, we consider the ODE

and regard the trajectory x(.) as the corresponding response of the system.
NOTATION. (i) We will write
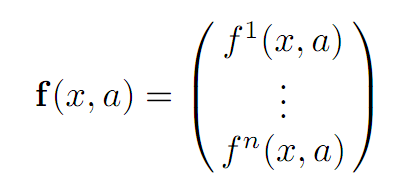
to display the components of f , and similarly put
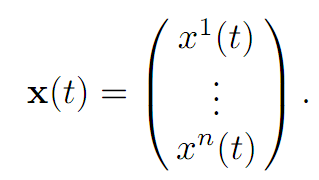
We will therefore write vectors as columns in these notes and use boldface for vector-valued functions, the components of which have superscripts.
(ii) We also introduce
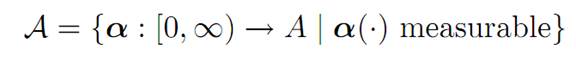
to denote the collection of all admissible controls, where
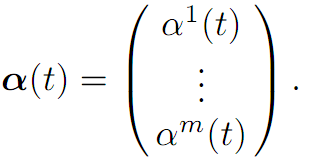
Note very carefully that our solution x(.) of (ODE) depends upon α(.) and the initial condition. Consequently our notation would be more precise, but more complicated, if we were to write

displaying the dependence of the response x(.) upon the control and the initial value.
PAYOFFS. Our overall task will be to determine what is the “best” control for our system. For this we need to specify a specific payoff (or reward) criterion. Let us define the payoff functional
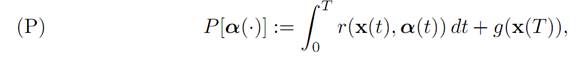
where x(.) solves (ODE) for the control α(.). Here r : Rn ×A → R and g : Rn → R are given, and we call r the running payoff and g the terminal payoff. The terminal time T > 0 is given as well.
THE BASIC PROBLEM. Our aim is to find a control α∗(.), which maximizes the payoff. In other words, we want

for all controls α(.) ∈ A. Such a control α∗(.) is called optimal.
This task presents us with these mathematical issues:
(i) Does an optimal control exist?
(ii) How can we characterize an optimal control mathematically?
(iii) How can we construct an optimal control?
These turn out to be sometimes subtle problems, as the following collection of examples illustrates.
References
[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.
[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.
[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.
[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.
[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.
[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.
[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.
[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.
[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.
[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).
[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.
[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.
[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.
[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.
[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.
[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.
[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.
[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.
[T] William J. Terrell, Some fundamental control theory I: Controllability, observability, and duality, American Math Monthly 106 (1999), 705–719.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|