


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-1-2021
Date: 2-1-2021
Date: 23-3-2016
|
NONLINEAR MATERIALS
What makes a material a good candidate as a harmonic light generator? That there are a number of coefficients governing the amount of harmonic light generated in relation to the fundamental. These nonlinear coefficients (a2 and a3), as well as the coefficient for the linear term (a1), are properties of the medium itself but can be determined and depend on the applied electric field. At small electric field values, the linear term dominates (i.e., the material behaves in, a linear manner), but as this value increases, the nonlinear coefficients increase as well, so the material behaves in a nonlinear manner. The linear term is related to the index of refraction by
a1 = ε0(n2 - 1) (1.1)
where ε0 is the permittivity of free space (8.85 × 10-12 F/m). This makes this term on the numerical order of 10-12 whereas the second-order coefficient a2 for many nonlinear crystals is on the order of 10-24. Table 1.1 lists the constants for actual crystals (the coefficients listed are in conventional MKS units, in which a2 is one-eighth of the coefficient listed since is actually a Taylor geometric series). Although this coefficient seems extremely small, consider that it is multiplied by E20 in the equation. For a small electric field such as E0 =1000 W/m (this is actually a reasonably bright light by everyday
TABLE 1.1. Nonlinear Optical Coefficients for Various Materials
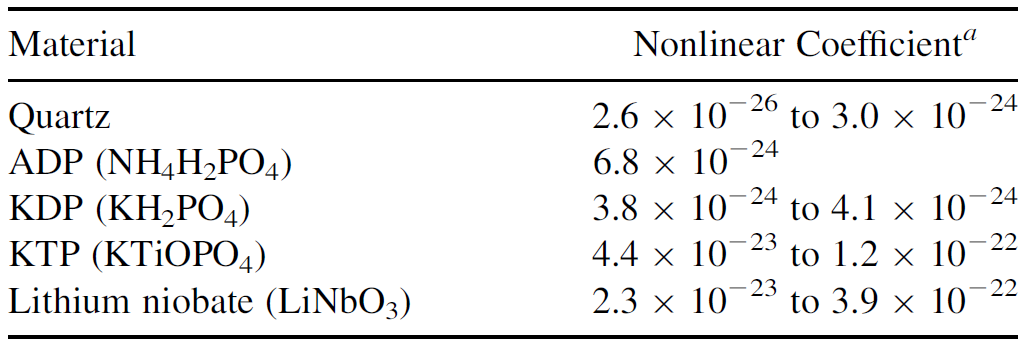
standards), the coefficient for the 2⍵ term is on the order of 10-18. This is extremely small compared to the a1 term, which is numerically on the order of 10-12 and hence 1 million times larger. The linear v term dominates and nonlinear activity is not seen. Now consider the situation when the applied electric field is large, as in that of a focused laser beam (say 106 W/m). The coefficient for the 2⍵ term is now] on the order of 10-12, about the same size as that of the ⍵ term. When applied electric fields are this large, the output of second-harmonic light from the crystal is also large.
Common crystals for use as frequency doublers have large nonlinear coefficients, but not all crystals in nature have this feature. Only crystals that have no symmetry have a nonzero a2 coefficient. These crystals are similar to those used in Pockels cell] EO modulators and are piezoelectric as well. An applied mechanical pressure will cause asymmetry and unequal distribution of charges in the crystal, and a DC voltage appears across the crystal. Piezoelectric crystals are commonly used to generate high voltages for sparks to ignite gas burners for barbecues and lighters. Quartz and other glasses have relatively small coefficients and hence make poor generators. Other crystals commonly used for harmonic generators that have large nonlinear coefficients include phosphates such as ADP (ammonium dihydrogen phosphate), KDP (potassium dihydrogen phosphate), KTP (potassium titanyl phosphate), and niobates such as lithium niobate (LiNbO3).
ADP and KDP were among the first nonlinear materials discovered. They are transparent from about 200 to 1500 nm but have a relatively small nonlinear coefficient. A better and more efficient material is KTP, which is more commonly used nowadays to double in Nd: YAG and Nd:YVO4 lasers. Lithium niobate is another common] material useful in the range 400 nm to 5 mm, making it more useful than ADP or KDP in the infrared. It has a large nonlinear coefficient, making it about 100 times more efficient than KDP as a second-harmonic generator. Table 1.1 lists some common nonlinear materials and their corresponding coefficients for comparison.
Commercially available nonlinear crystals are often specified by the type of phase-matching required, phase-match angle, and coatings on the crystal faces. In general, crystal faces must be coated with antireflective coatings suitable for both the fundamental and harmonic wavelength involved. An uncoated crystal would lead to a large intracavity loss, which may well prevent oscillation of the laser.

Figure 1.1. Damage to a nonlinear crystal.
Finally, a good nonlinear crystal must be able to take the enormous power densities incident on the crystal without permanent damage. As shown in Figure 1.1, a nonlinear crystal may be damaged when the incident power reaches a high enough level. In this particular case, heat generated by the incident laser beam caused the crystal to fracture. Each type of crystal then has a characteristic damage threshold, which varies from 20 MW/cm2 for a lithium niobate crystal (which has a particularly low damage threshold) to 500 MW/cm2 for an ADP crystal (which has one of the highest damage thresholds of any nonlinear material). Damage is, of course, a concern since the intracavity beam of a Q-switched laser can possess as high a power density as the focused beam of any laser.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
في مستشفى الكفيل.. نجاح عملية رفع الانزلاقات الغضروفية لمريض أربعيني
|
|
|