ANGULAR  MOMENTUM  IN  QUANTUM  STATES

Number n, which in the Bohr model represented an orbit. If we are to continue using the analogy of an electron as an orbiting satellite around a planet, we must also account for the angular momentum of the satellite. By knowing the total kinetic energy and the total angular momentum of a planet, we may predict its orbit and energy. Refining the analogy even further, planets have two types of angular momentum: orbital and spin. The spin is an intrinsic angular momentum; in the case of the Earth, it is the spin of the planet that brings about day and night. Furthermore, the orbiting satellite in our case, a charged electron generates a magnetic field by virtue of the fact that we have a moving charge. Both effects, magnetic and spin, contribute to the complete description of an energy state, but the largest influence is that of the orbital angular momentum of the electron, so we shall deal with it first. One major shortcoming of the Bohr model was the failure to account for the hyperfine structure of hydrogen lines. Each line emitted from hydrogen is, in fact, a series of very closely spaced lines. In 1916, the physicist Arnold Sommerfeld suggested that orbiting electrons could follow not only a circular orbit (as in the Bohr model) but also elliptical orbits, and each orbit would have a slightly different energy than that of the circular orbit. His theory was that only certain elliptical orbits would be allowed in the atom fitting the requirements for quantization in the atom. A set of allowed orbits, then, would exist for each principal quantum number n. In the case of the hydrogen emission spectrum, transitions between these closely spaced energy levels give rise to the many closely spaced lines seen. Every particle in orbit has a constant angular momentum in that orbit equal to its mass times its velocity (where velocity is a vector quantity having the property of direction). The same is true whether an orbit is circular (in which case l = mv) or noncircular (in which case L = mvr sin θ). The later case is depicted in Figure 1.1, where angular momentum is the same at every point in the orbit of the particle. When the particle approaches the center (at radius r₂ in the figure), speed increases; when

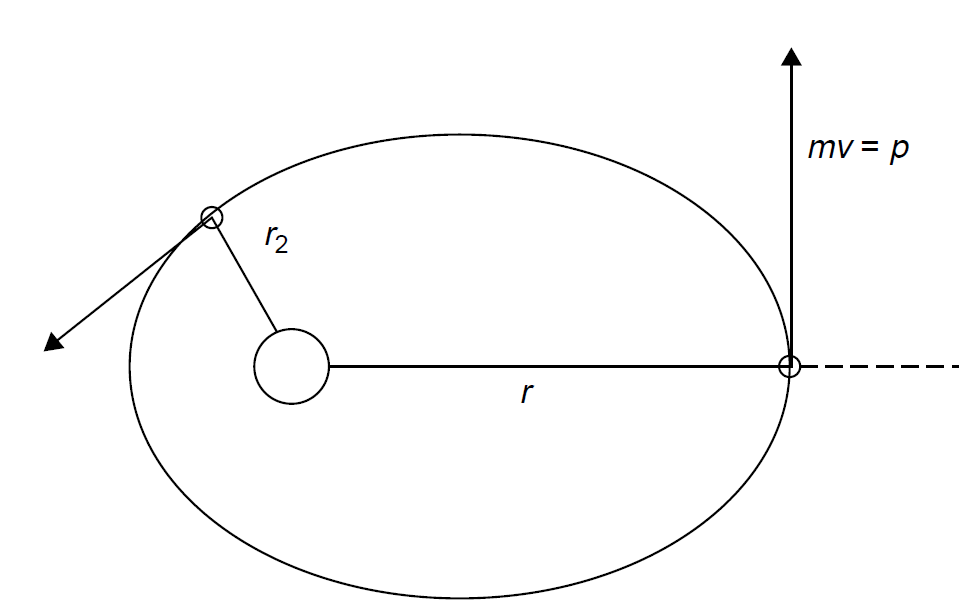
Figure 1.1. Angular momentum of a particle.

the radius is larger, the speed is lower. This is simply conservation of momentum, a concept from basic kinematics, which holds true here as well. By analogy, electrons orbiting around a nucleus will also exhibit angular momentum. Having angular momentum implies that the electron has kinetic energy whose amount is limited by the total electron energy (in the case of an atom, the total energy is described by the principal quantum number n). Like other quantities in an atom, angular momentum is quantized into allowed values; this is one result of the solution of wave equations (Schrodinger wave equations), which describe the behavior of the electron. Angular momentum consists of two key components: orbital angular momentum and spin angular momentum. Spin is an intrinsic property of electrons and is manifested by the magnetic moment created by spinning electrons. Orbital angular momentum is somewhat more straightforward from a classical perspective and is examined first. We now introduce a quantum number, l, to describe orbital angular momentum. This number, the orbital quantum number, describes the magnitude of the orbital angular momentum. Values for l are constrained by the principal quantum number n and can have integer values of zero to n -1. For a principal quantum number of n = 1, l always has a value of zero. This indeed states that the lowest orbit has an angular momentum of zero—at odds with Bohr’s original model! For a principal quantum number of n = 2, l can be 0 or 1, meaning that an electron in the n = 2 state can have zero angular momentum, corresponding to a circular orbit, or some discrete value of angular momentum, corresponding to an elliptical orbit. In either case (=0 or 1), the electrons have almost the same energy (i.e., they are still both in the n =2 principal state). Both quantum numbers together, n and l, are required to fully describe the energy of a given state.