The Wave Equation

The one-dimensional, nonrelativistic Schrodinger's wave equation is given by

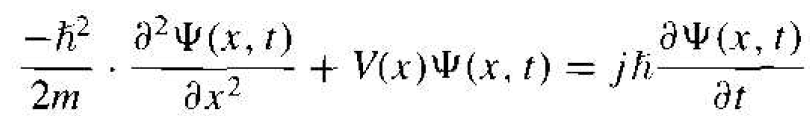(1)

where Ψ (x, t) is the wave function, V(x) is the potential function assumed to be independent of

time, m is the mass of the particle, and j is the imaginary constant 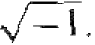. There are theoretical arguments that justify the form of Schrodinger's wave equation. hut the equation is a basic postulate of quantum mechanics. The wave function Ψ (x, t) will be used to describe the behavior of the system and, mathematically, Ψ (x, t) can be a complex quantity.

We may determine the time-dependent portion of the wave function and the position-dependent, or time-independent, portion of the wave function by using the technique of separation of variables. Assume that the wave function can he written in the form

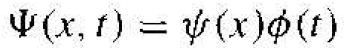(2)

where ѱ(x) is a function of the position x only and ϕ(t) is a function of time t only. Substituting this form of the solution into Schrodinger's wave equation, we obtain

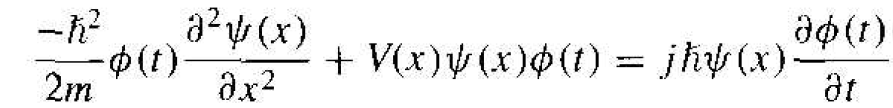(3)

If we divide by the total wave function. Equation (3) becomes

(4)

Since the left side of Equation (4) is a function of position x only and the right side of the equation is a function of time t only, each side of this equation must he equal to a constant. We will denote this separation of variables constant by η.

The time-dependent portion of Equation (4) is then written as

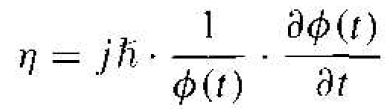(5)

where again the parameter η is called a separation constant. The solution of Equation (5) can be written in the form

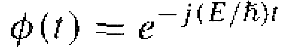(6)

The form of this solution is the classical exponential form of a sinusoidal wave where η/h is the radian frequency ω. We have that E = hv or E = hω/2π. Then ω = q/h = E/h so that the separation constant is equal to the total energy E of the particle.

The time-independent portion of Schrodinger's wave equation can now he written from Equation (4) as

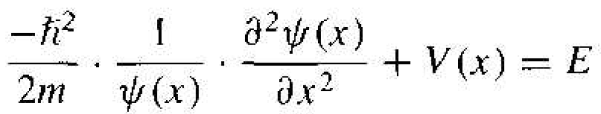(7)

where the separation constant is the total energy E of the particle. Equation (7) may he written as

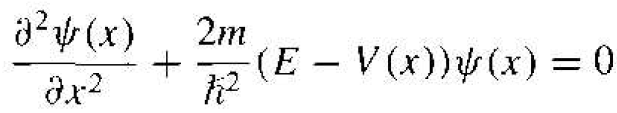(8)

where again m is the mass of the particle, V(x) is the potential experienced by the particle, and E is the total energy of the particle. This time-independent Schrodinger's wave equation can also be justified on the basis of the classical wave equation as shown in Appendix E. The pseudo-derivation in the appendix is a simple approach but shows the plausibility of the time-independent Schrodinger's equation.