


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | المتجهات في فضاء البعد الثاني وفضاء البعد الثالث-المقدمة والمعنى الهندسي للمتجهات |
|
|
|
أقرأ أيضاً
التاريخ: 20-3-2016
التاريخ: 8-3-2016
التاريخ: 1-3-2016
التاريخ: 19-3-2016
|
المقدمة والمعنى الهندسي للمتجهات
لهذا الموضوع تطبيقات مهمة وكثيرة، فعلى سبيل المثال تظهر في الفيزياء كميات مثال الساحة، الطول، دراجات الحرارة يعبر عنها بقيمتها العددية فقط. وهناك كميات أخرى يعبر عنها بقيمتها العددية واتجاهها، كالقوة والسرعة وحركة الريح فمثلاً حركة الريح يعبر عنها من خلال معرفة سرعتها واتجاهها. هذه الكميات تمثلها بشكل متجه.
المعنى الهندسي للمتجهات:
يمكن التعبير عن المتجهات بشكل خطوط مستقيمة اتجاهية أو بشكل أسهم. السهم يمثل اتجاه المتجه أما طول السهم فيمثل قيمته. بداية السهم يقال لها نقط بداية المتجه وقمة السهم تسمى نقطة النهاية أو الرأس. في الشكل المجاور نقطة البداية للمتجه v هي النقطة A ونقطة النهاية هي B ونكتبه:

متجهات متكافئة (b)
شكل (1-1)
المتجهات التي لها نفس الطول والاتجاه تسمى متجهات متكافئة وتكتب v = u للتعبير عن تكافؤ المتجهات v و u.
ملاحظة:
المتجه v ذي الطول والاتجاه يكتب احياناً 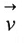 والسهم يعبر عن الاتجاه. خلال هذا الكتاب سنكتب المتجه .... بالشكل v ونسميه المتجه v.
والسهم يعبر عن الاتجاه. خلال هذا الكتاب سنكتب المتجه .... بالشكل v ونسميه المتجه v.
تعريف (1-1):
إذا كانت u , v أي متجهين فإن جمعها v + u هو متجه يعبر عنه هندسياً كما يلي: نضع نقطة بداية u على نهاية المتجه v. المتجه v + u يمثل بسهم من بداية v إلى نهاية u ، في الشكل (1-2) يوجد جمعان v + u و u + v وكلاهما متساويان أي، v + u = u + v والجمع يمثل هندسياً بقطر متوازي الأضلاع.
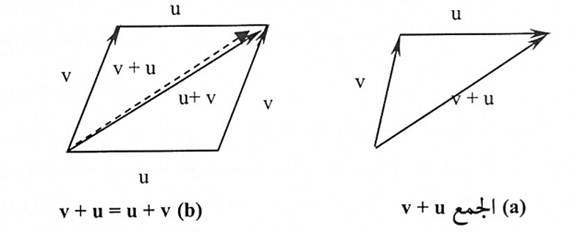
شكل (1-2)
المتجه الذي طوله يساوي صفر يسمى المتجه الصفري ويكتب بالشكل 0 ويعرف v + 0 = 0 + v = v لكل متجه v .
إذا كان v متجه غير صفري فإن –v يعرف بأنه سالب v وهو متجه طوله مساوياً لطول v ولكن بعكس الاتجاه. هذا المتجه يحقق الخاصية v + (-v) = 0.
لاحظ الشكل (1-3) .
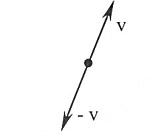
شكل (1-3)
تعريف (1-2):
ليكن v و u متجهين فإن الفرق بينهما يعرف بالصيغة:
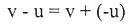
لاحظ الشكل (1-4)b.
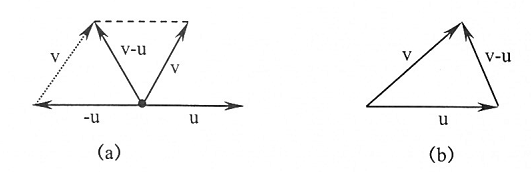
شكل (1-4)
ولتعيين v – u تطابق نقطتي البداية لكل من v و u على بعضهما كما في الشكل (1-4)b المتجه الواصل بين نهاية المتجه u إلى نهاية v هو المتجه v-u.
تعريف (1-3): ليكن v متجه غير صفري و k كمية ثابتة (عدد حقيقي) غير صفرية فإن الضرب kv هو متجه طوله |K| مضروب طول v واتجاهه هو نفس اتجاه v، إذا كان k>0 اما إذا كان k<0 فاتجاهه معاكس لاتجاه v. كما ونعرف kv = 0 إذا كان K = 0 أو v = 0. (-1)v هو متجه طوله يساوي طول v لكن باتجاه معاكس ويمكن كتابته (-1)v = -v.
ليكن v متجه مرسوم في المستوى ولتكن بدايته نقطة الأصل لأي احداثيين متعامدين، لاحظ الشكل (1-5).
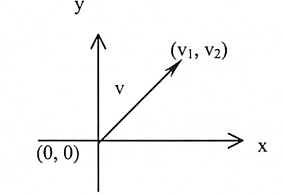
شكل (1-5)
نفرض إحداثيات نقطة نهاية v هما (v1 , v2)، يقال للإحداثيين v1 و v2 بمركبتي المتجه v ويكتب v بالصيغة:
V=(v1,v2)
إذا كان v = (v1 , v2) و u = (u1 , u2) فإن v تكافئ u إذا وفقط إذا v1 = u1 و v2 = u2.
أما v + u فيعرف بأنه:

لاحظ الشكل (1-6).
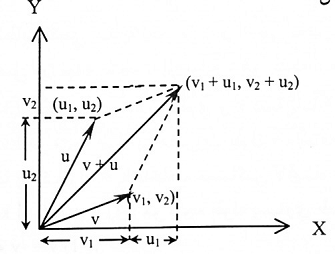
شكل (1-6)
إذا كان v = (v1 , v2) و K كمية ثابتة فإن kv (شكل 1-7)
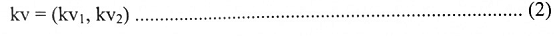

شكل (1-7)
مثال(1):
لتكن v = (-2,1) و u = (3,4) فإن:
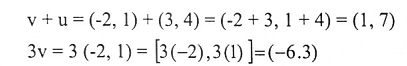
وبما أن v –u = v +(-1)u وباستخدام خاصتي الجمع والضرب نحصل على:
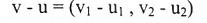
مثال(2):
لتكن v و u كما في المثال فإن:
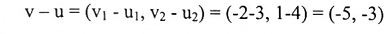
لما كانت المتجهات في المستوى يمكن التعبير عنها بزوج من الأعمدة الحقيقية فإن المتجهات المرسومة في الفضاء الثلاثي يمكن تمثليها بثلاث من الأعمدة الحقيقية وذلك من خلال تكوين نظام إحداثي وكما يأتي:
نعين نقطة مثل 0 ونسميها نقطة البداية وتكون ثلاث مستقيمات متعامدة تسمى المحاور الإحداثية تمر بنقطة ونرمز لهذه المحاور بالرموز y و z بعد تعين الاتجاهات الموجبة واختيار وحدة القياس المسافات. لاحظ أن كل محورين يعينان مستوى يسمى المستوى الإحداثي وهي المستوى xy-، المستوى xz- والمستوى yz-. لذا فإن أي نقطة مثل p يمكن تمثليها بالثلاثي (x,y,z) من الأعمدة الحقيقية ويسمى إحداثي النقطة p، لاحظ (الشكل (1-8).
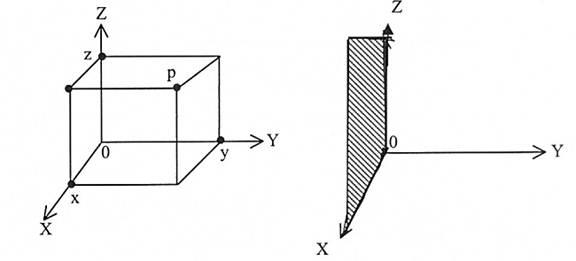
شكل (1-8)
عليه فإن إحداثي النقطة p هي x = 0x ، y = 0y و z = 0z.
إذا أردنا رسم المتجه v في الفضاء الثلاثي نضع بدايته في نقطة الأصل 0، فإن إحداثيات نقطة نهايته تسمى مركبات v وتكتب:
V=(x,y,z)
مثال(3):
ارسم النقطة p التي إحداثياتها (3,4,5)
الحل:
لاحظ الشكل (1-9).
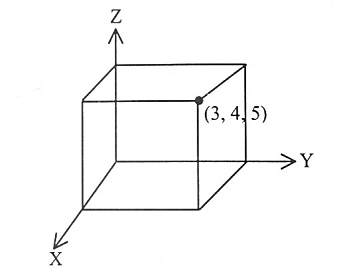
شكل (1-9)
لتكن V = (v1 , v2, v3) و u = (u1, u2, u3) متجهات في فضاء 3-، فإن بالإمكان الحصول على صيغ مشابهة لتلك في فضاء 2- وهي:

مثال(4):
نفرض أن v = (-1,3,2) ، u = (4,1,2)


ملاحظة: في بعض الأحيان لا تقع بداية المتجه في نقطة بداية المحاور وفي هذه الحالة تسمى بالمتجهات الحرة والمتجهات التي بدايتها تنطبق على نقطة الأصل فتسمى بالمتجهات المقيدة.
إذا كانت نقطة بداية المتجه p1p2 هي p1 (x1 , y1 , z1) ونقطة نهايته هي p2 (x2,y2,z2) فإن المتجه p1p2 يعرف بالشكل:
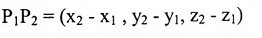
أي أن مركبات p1p2 هي عبارة عن مركبات نهايته مطروحاً منها مركبات بدايته أي:
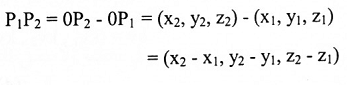
مثال(5):
ليكن v = p1p2 متجه نقط بدايته النقطة p1 (3,-1,4) ونقطة نهايته p2 (5,-2,4) فإن مركباته هي:
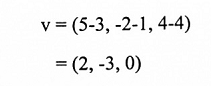

شكل (1-10)
إزاحة المحاور: في حالات معينة حلول التمارين تحتاج القيام بإزاحة محاور الإحداثيات للحصول على محاور جديدة موازية للمحاور الأصلية ففي الشكل (3-11) قمنا بإزاحة المحاور للنظام الإحداثي xy- للحصول على النظام الإحداثي x'y,- الذي نقطة الأصل قيمة هي 0' تقع على النقطة (x , y) = (h, k) لذا فإن إحداثيات النقطة p في افضاء الثنائي هي (x , y) و (x', y'). ولكي نبرهن كيف ان هذه الإحداثيات مرتبطة مع بعضها البعض، نأخذ المتجه 0'P شكل (1-11)، في النظام xy- نقطة بدايته هي (h , k) ونقطة نهايته على (x , y). لذا فإن 0'P = (x-h , y-k) . أما في النظام x'y' فنقطة بدايته على (0,0) ونهايته على (x',y')، أي أن:
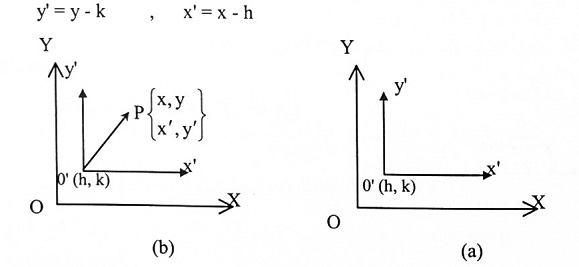
شكل (1-11)
الصيغ x' = x-h و y' = y-k تسمى معادلة الإزاحة.
مثال(6):
نفرض أن النظام الإحداثي xy- أزيح للحصول على النظام الإحداثي x'y' الذي نقطة أصله في الإحداثيات xy- هي (3,1) = (h,k)
a. اوجد النقطة في الإحداثيات x'y' إذا كانت إحداثياتها xy' هي p(1,0).
b. أوجد النقطة في الإحداثيات xy- إذا كانت إحداثياتها x'y'- هي Q (-1,4).
الحل:
a. معادلة الإزاحة هي:
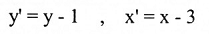
لذا فإن الإحداثيات x'y'- للنقطة p(1,0) هي:
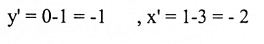
b. معادلات الإزاحة في الحالة (a) يمكن كتابتها على الشكل:

لذا فإن الإحداثيات xy- للنقطة Q هي:
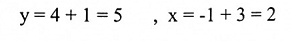
ملاحظة:
في الفضاء 3- معادلات الإزاحة هي:
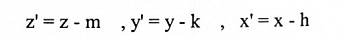
حيث (h ,k, m) هي إحداثيات xyz- لنقطة الأصل x'y'z'.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|