

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
المحددات-النشر بواسطة العامل المرافق، قاعدة كرام
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
112-124
8-3-2016
33895
النشر بواسطة العامل المرافق، قاعدة كرامر:
نتطرق في هذا البند إلى طريقة مهمة ومفيدة لحساب المحددان، ونتيجة لعملنا هنا سنحصل على صيغة لمعكوس المصفوفة القابلة للانعكاس، إضافة إلى صيغة لحل أنظمة خطية معينة بلغة المحددات.
تعريف (1-1):
مصغر العنصر aij في المصفوفة المربعة، يكتب ،Mij، هو محدد المصفوفة الجزئية الناتجة من حذف الصف رقم i أو العمود رقم j في المصفوفة A العدد (-1)i+j Mij، يكتب Cij، يعرف بأنه العامل المرافق للعنصر aij .
ملاحظة:
نلاحظ من خلال التعريف أعلاه أن المصغر والعامل المرافق للعنصر aij يختلفان فقط بالإشارة أي أن، Cij =± Mij
وبما أن الإشارات تأتي بشكل متناوب وأن إشارات القطر الرئيسي دائماً موجبة ولسهولة حفظ هذه الإشارات ومواقعها يمكننا عمل الشكل الآتي:
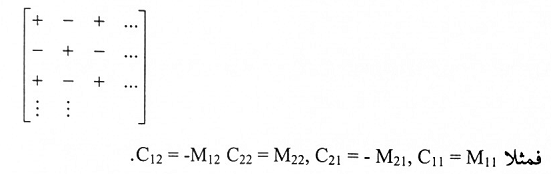
مثال(1):

النشر بالعوامل المرافقة:
من المثال (7) في)داله المحدد) إذا كانت
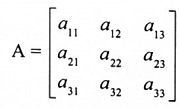
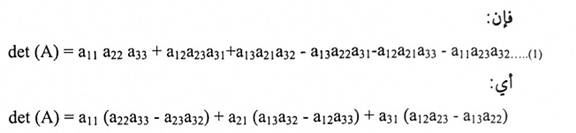
ولما كانت المقادير المحصورة بين قوسين تمثل العوامل المرافقة C31, C21, C11 على التوالي، فإن:
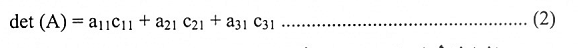
تبين المعادلة اعلاه أن محدد A يمكن إيجاده بجمع نواتج ضرب عناصر العمود الاول للمصفوفة A في مرافقاتها ومن ثم جمع نواتج الضرب.
طريقة حساب محدد A هذه تسمى النشر بالعوامل المرافقة بواسطة العمود الاول.
مثال(3):
نفرض
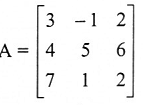
احسب |A| باستخدام طريقة النشر بالعوامل المرافقة بدلالة الصف الأول.
الحل: نجد العوامل المرافقة لعناصر الصف الأول في A.
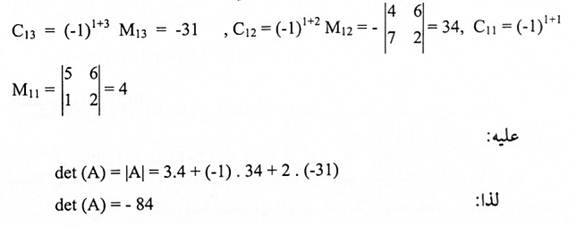
ملاحظة:
1. يمكن إجراء النشر بالمرافق بدلالة أي صف أو أي عمود من المصفوفة A.
2. بالإمكان تعميم المعادلة (1) للمصفوفة A التي سعتها n x n.
3. أن أفضل طريقة للنشر تتم بدلالة الصف أو العمود الذي يحتوي على أكبر عدد من الأصفار فإذا كان aij = 0 ففي هذه الحالة لا تحتاج للمقدار Cij.
مثال(3) :
احسب محدد المصفوفة A
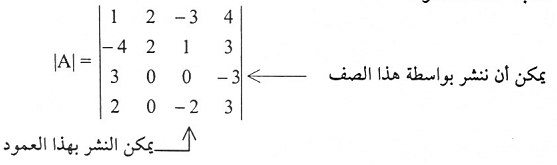
لاحظ أن من الأفضل النشر بدلالة الصف الثالث أو العمود الثاني لأن كل منهما يحتوي على أكبر عدد من الأصفار. نسب المحدد بدلالة الصف الثالث.


النتائج التي حصلنا عليها بالنسبة للمصفوفة التي سعتها 3 ×3 تمثل حالة خاصة من المبرهنة العامة الآتية والتي سنذكرها بدون برهان.
مبرهنة (1-2):
يمكن حساب محدد المصفوفة التي سعتها n x n، بجمع حاصل ضرب عناصر أي صف (عمود) بعواملها المرافقة.
أي أن لكل
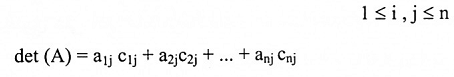
هذه العلاقة تمثل نشر العوامل المرافقة بدلالة العمود j.
أما
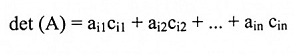
فتمثل النشر بدلالة الصف رقم i.
تعريف (1-3):
إذا A مصفوفة سعتها n × n و Cij العامل المرافق للعنصر aij ، فمصفوفة العوامل المرافقة هي:

المصفوفة المصاحبة لـ A، يرمز لها (A) adj، هي منقولة مصفوفة العوامل المرافقة. أي :
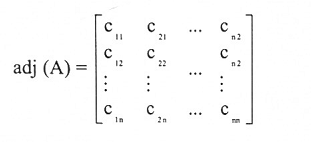
مثال (4):


مبرهنة (1-3):
إذا كانت A مصفوفة قابلة للانعكاس فإن:

البرهان:
نبرهن أولاً أن A. adj (A) = |A|. In
باستخدام قاعدة ضرب المصفوفات نحصل على:
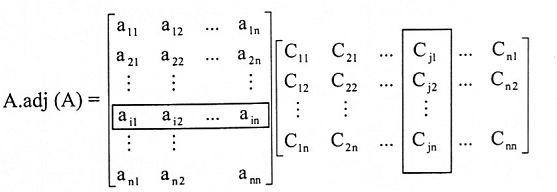
العنصر في الصف رقم i والعمود j في حاصل ضرب A. adj (A) هو:

إذا كان I = j فإن (4) تمثل النشر بالعامل المرافق لمحدد A بدلالة الصف رقم i في المصفوفة A (مبرهنة 1-2).
أما إذا I ≠ j فإن (4) يجب أن تساوي صفر لأن العناصر a's والعوامل المرافقة تأتي من صفوف A المختلفة. عليه فإن قيمة (4) تساوي صفر.

مثال(5):
استخدم الصيغة (6) لإيجاد معكوس المصفوفة
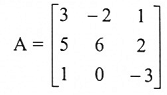
الحل:
توجد محدد A أولاً باستخدام العلاقة (6) والمثال (3):
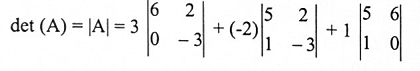
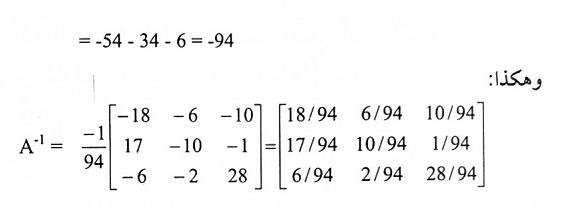
مثال (6):
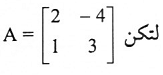
احسب A-1 إن وجدت مستخدما العلاقة (3).
الحل:
1. نحسب محدد A:
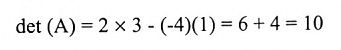
بما أن محدد A يساوي 10 ، فإن A قابلة للانعكاس.
2. نجد المصفوفة المرافقة

3. مصفوفات المرافقات:
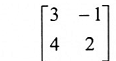
4. عليه 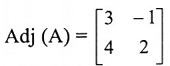 adj (المصفوفة المصاحبة)
adj (المصفوفة المصاحبة)
5. نستخدم العلاقة
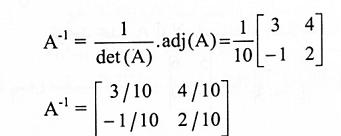
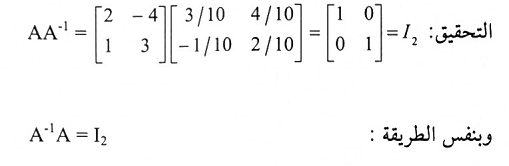
قاعدة كرامر:
المبرهنة التالية ستقدم صيغة أخرى من الصيغ المهمة في حل أنظمة المعادلات الخطية التي تحتوي على n من المعادلات و n من المتغيرات هذه الطريقة مهمة أيضاً من خلال دراسة خواص حلول الأنظمة الخطية دون الحاجة للدخول في تفاصيل الحل الطويلة.
مبرهنة (1-4): ليكن AX = B نظام خطي يحتوي على n من المعادلات و n من المتغيرات بحيث أن det (A) ≠ 0، فإن هناك حلاً وحيداً للنظام . هذا الحل هو:
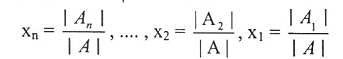
حيث أن (j = 1,2, … , n) هو المصفوفة التي نحصل عليها باستبدال عناصر العمود رقم j في المصفوفة A بعناصر المصفوفة B حيث:
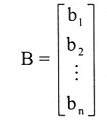
البرهان:
بما أن |A| ≠ 0 ، فإن A قابلة لانعكاس، وبموجب مبرهنة X = A-1B هو الحل الوحيد للنظام AX = B
لذا وبموجب المبرهنة (1-3) نحصل على:

بما أن Aj تختلف عن A فقط في العمود j، فإن العوامل المرافقة للعناصر b1 , b2, … bn في Aj هي نفسها العوامل المرافقة المقابلة لعناصر العمود j في A.
لذا بنشر المحدد|Aj| بعناصر العمود رقم j نحصل:
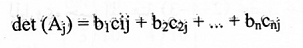
بتعويض هذه النتيجة في: ((7 نحصل على :
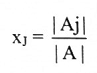
مثال(7):
باستخدام قاعدة كرامر حل النظام الخطي:
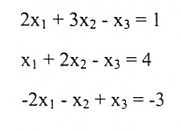
الحل:
نجد محدد المصفوفة A:
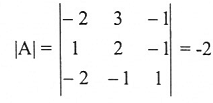
وباستخدام قاعدة كرامر:
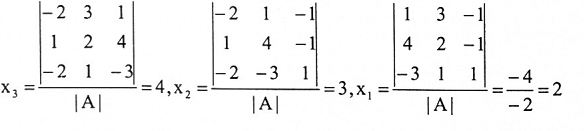
مثال(8):
حل النظام الآتي:
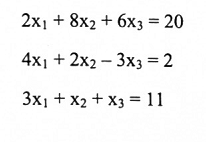
الحل:
نجد محدد A:

 الاكثر قراءة في الجبر الخطي
الاكثر قراءة في الجبر الخطي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















