يهدف هذا البند إلى استنتاج بعض الصفات الأساسية للتحويلات الخطية العامة.

مبرهنة (1-1):

لتكنW⟶T :V  تحويلة خطية، فإن مجموعة جميع المتجهات في V التي صورة كل منها بواسطة T تساوي صفر تسمى نواة T وتكتب (kernel T) Ker T. اما مجموعة جميع المتجهات في W والتي هي عبارة عن صورة لعلى الأقل متجه واحد في V بواسطة T، تسمى مدى T، وتكتب     (Image T) Im(T).

يمكن تعريف كل من Ker (T) و Im (T) جبرياً على النحو الآتي:

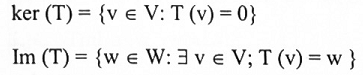
مثال(1) :

لتكن T:R³⟶R³ تطبيق إسقاطي والمعرف بالشكل:

أوجد Ker T  و  Im T

الحل:

واضح ان النقاط على المحور z تكون صورتها بواسطة T هي المتجه الصفري 0 لذا فإن أما صورة T فتتكون من جميع النقاط في المستوى xy، أي،

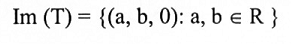
مثال(2):

لتكن W⟶T:V تطبيق خطي فإن Ker (T) فضاء جزئي في V و Im (T) فضاء جزئي في W.

الحل:

بما أن T(0) = 0 فإن 0∊ker T (أي أن Ker T غير خالية).

نفرض . ∊ker T u,v إذن T(v) = 0  و  T(u) = 0. لذا فإن:

إذن Ker T فضاء جزئي في V.

وبنفس الطريقة شرط الضرب.

مثال(3):

لتكن T:R⁴⟶R³ تحويلة خطية معرفة بالشكل:

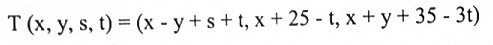
أوجد أساس وبعد صورة T.

الحل: نوجد صور المتجهات الطبيعية للفضاء R⁴.

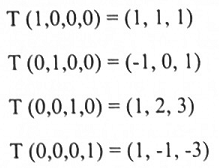
عليه فإن متجهات صور T تنشأ (T) Im (صورة T). بوضع هذه المتجهات بشكل صفوف وبموجب الشكل المدرج الصفي المختزل نحصل على: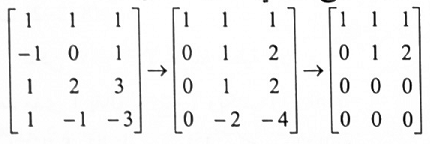                                                                                         

لذا فإن : {(1,1,1) , (0,1,2)} أساس Im (T).

عليه فإن بعد Im (T) هو 2.

مثال(4):

أوجد أساس وبعد Ker (T) للتحويلة الخطية في المثال 3.

الحل:

نفرض T(v) = 0 حيث v = (x,y,s,t)

أي:

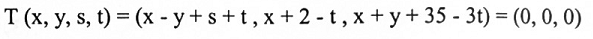
 وبمقارنة مركبات المتجهات لطرفي المعادلة أعلاه نحصل على:

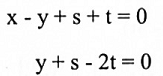
حيث t, s هي المتغيرات الحرة، لذا فإن بعد النواة هو 2.

وبإعطاء قيم لأعلى التعين لـ t, s كالآتي:

عندما s = -1  و  1= 0 نحصل على الحل: (2, 1,-1,0).

وعندما s = 0  و  t = 1 نحصل على الحل: (1,2,0,1).

لذا فإن: {(2,1,-1,0) , (1,2,0,1)} هو أساس Ker (T)

لقد عرفنا في البند رتبة المصفوفة بأنه بعد فضاء أعمدتها وصفرية المصفوفة بأنها بعد فضائها الصفري. سنحاول الآن تعميم هذه التعاريف على التحويلات الخطية العامة.

تعريف (1-2):

لتكن W⟶T:V تحويلة خطية فإن:

1. بعد مدى T يقال له رتبة T ويكتب rank (T).

2. بعد نواة T يقال له صفرية T  ويكتب null (T).

مبرهنة (1-2):

إذا كانت A مصفوفة سعتها m x n  و  T_A:Rⁿ⟶R^m مضروبة A فإن:

1. صفرية (T_A) = صفرية (A).

2. رتبة (T_A) = رتبة (A).

البرهان:

لما كانت A سعتها m x n  و T_A:Rⁿ⟶R^m مضروبة A وبموجب المناقشات في الفصول السابقة فإن نواة T_A هي فضاء A الصفري.

ومدى T_A هو فضاء أعمدة A.

مثال(5):

لتكن T:R⁴⟶R⁴ مضروبة A. أوجد رتبة وصفرية T_A

حيث:

الحل:

من المثال 8 في (رتبه المصفوفه) وجدنا أن رتبة A هي 3 وصفرية A هي 1. لهذا وبموجب مبرهنة (1-3) نحصل على

رتبة T_A هي 3 وصفرية T_A هي 1.

مبرهنة (1-4):

لتكن W⟶T:V تحويلة خطية من فضاء المتجهات الذي بعده n إلى فضاء المتجهات W فإن:

(1) .......................................... رتبة T + صفرية n = T

أو:

                                                          N =rank (T) + null (T)

أو:

                                                بعد مدى T + بعد نواة n = T

مثال(6):

من الأمثلة 3 و 4 وجدنا أن بعد مدى T هو 2 وبعد نواة T هو 2 وبموجب مبرهنة (1-4) نجد أن:

رتبة T + صفرية 4 = 2+2 = T وهذه تساوي بعد منطلق T.

مثال(7):

من المثال(1) وجدنا ان بعد مدى T هو 1 وبعد نواتها هو 2 لذا فإن:

2+1 = 3 وهو عبارة عن بعد منطلق T.

أي أن:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام- فضاء المتجهات الحقيقي

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي