


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 28-2-2016
Date: 2-12-2015
Date: 2-12-2015
|
Stress Effects
The Wulff–Kaichew theorem implicitly assumes that the crystal and substrate have the same crystal lattice, i.e., the same structure and the same lattice parameter. In practice, this is rarely the case. The crystal may than be distorted to fit onto the substrate lattice, thereby creating interface stresses. The stored elastic energy must then be taken into account when calculating the equilibrium shape of the supported crystal. This problem has only been tackled recently Muller and Kern(1) gave an analytic solution in a simplified case, using the laws of elasticity. They considered a parallelipiped equilibrium shape with base l and height H. Figure 1. shows half the crystal in profile. The continuous curves represent the loci of the upper edge as a function of the size for different values of the lattice mismatch m (Fig. 1a).
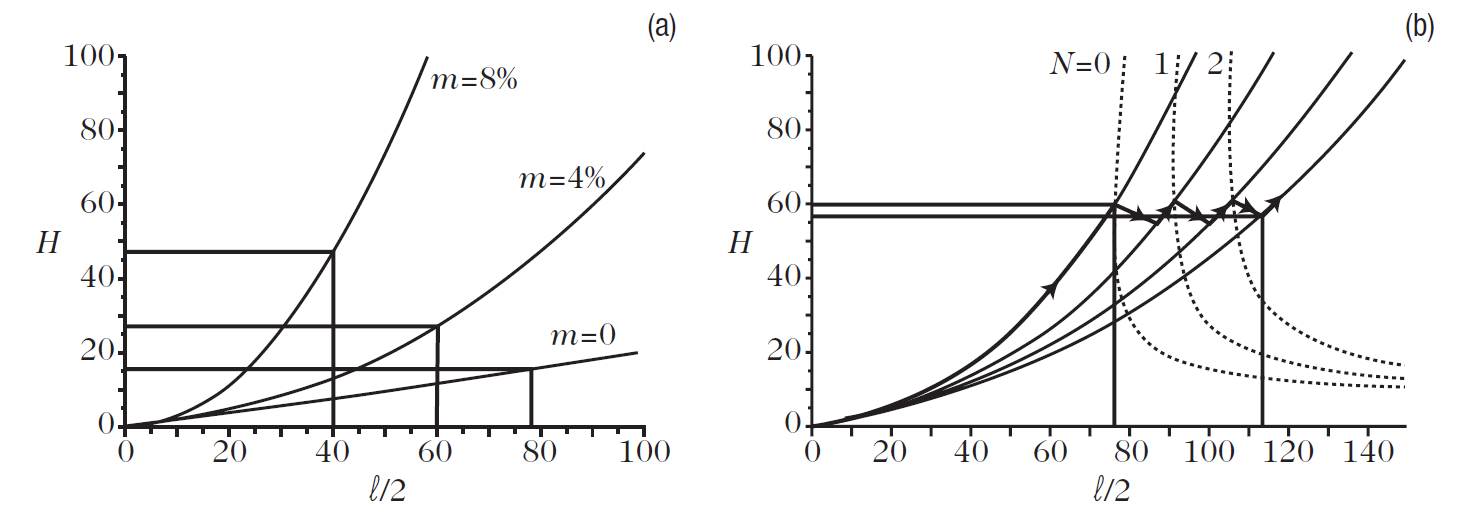
Fig. 1. Equilibrium shapes of stressed crystals. The profile of the crystals is represented for different values of the lattice mismatch m. Continuous curves represent the locus of intersection of the upper edge with the plane of the figure. (a) Stressed crystals. (b) Above a critical size, the crystals relax plastically through the successive appearance of dislocations. Dotted curves represent the thermodynamic criterion for the appearance of dislocations of order N (= 0, 1, 2, . . .). Taken from M¨uller and Kern (1)
The lattice mismatch is equal to the difference between the values of the lattice parameters divided by the value of the lattice parameter for the substrate. For perfect lattice matching (m = 0), we obtain a straight line (seeFig. 1a), which indicates that the aspect ratio (the ratio H/l of the height to the size) is constant, i.e., the equilibrium shape is independent of the size. We then recover the Wulff (or Wulff–Kaichew) theorem. For nonzero lattice mismatch, the aspect ratio is no longer constant. In fact it grows with the size of the crystal, i.e., the equilibrium shape does now depend on the crystal size.
Moreover, the greater the lattice mismatch, the more the aspect ratio will increase. This result can be understood quite simply from the fact that the crystal tries to reduce the stresses, localised near the interface, by reducing the area of that interface. However, when the size of the crystal increases, the stored elastic energy increases and, at some point, it becomes more economical energywise to undergo plastic relaxation by creating dislocations.
Figure 1.b shows that, beyond a certain size, the crystal relaxes by emitting a dislocation. The upper edge then moves toward a curve corresponding to a lower lattice mismatch, before a second dislocation is introduced and the process starts over again. It can be seen that the height of the crystal oscillates around a certain value. This process will continue until a regular network of interface dislocations has been created which relaxes the crystal toward its normal lattice parameter.

Fig. 2. Molecular dynamics simulation for Pd/MgO (100). Equilibrium shape of a 5-nm cluster.
Very recently, this problem of the equilibrium shape of stressed crystals has been studied for a specific system, Pd/MgO (100), using molecular dynamics simulation. For Pd, the authors used a semi-empirical potential based on the tight-binding method in the second moment approximation, where the electron density of states is characterized only by the average bandwidth, which provides a good representation of the transition metals. To simulate the Pd–MgO interaction, potential curves had to be constructed using ab initio energy calculations. Using these potentials, the authors were able to simulate Pd crystals of different sizes, treating the support as fixed. Figure 2 shows the equilibrium shape obtained for a 5-nm Pd particle. The equilibrium shape is indeed that of the truncated Wulff polyhedron. The calculation gives the adhesion energy directly. This energy is graphed as a function of the size of the Pd cluster in Fig. 3a. As the size of the Pd particle increases, the adhesion energy drops (in absolute value), starting from a value of about 1 J/m2 (this energy being graduated in eV per atom in Fig.3a), down to a roughly constant value of 0.85 J/m2. Below a size of about 7 nm, this trend is no longer followed monotonically. For sizes of about 3.5 and 7 nm, there are minima as indicated by the arrows in the figure. Figure 3.d shows the occupation percentage of oxygen sites on the substrate, these being the most favorable absorption sites for isolated atoms or a monolayer pseudomorphic to the substrate. The drop in (the absolute value of the) adhesion energy corresponds to a reduction in occupation of the oxygen sites. This is easily understood from the fact that the metal–substrate binding energy is maximal at oxygen sites, so that the total energy of metal–substrate bonds, which represents most of the adhesion energy, is then reduced (see Fig. 3b). But how do we explain these strange minima in the adhesion energy? We can obtain a better understanding of what is happening if we examine Fig. 4, which shows variations of the lattice parameter in the first Pd layer, at the interface, in the directions parallel and perpendicular to the substrate. Parallel to the substrate, the Pd lattice is dilated, which one would have expected, since Pd has an fcc structure like MgO, but with an 8% smaller lattice parameter. The contraction in the direction perpendicular to the interface respects the tetragonal deformation predicted by the theory of elasticity. Note, however, that these deformations are not uniform throughout the Pd particle.
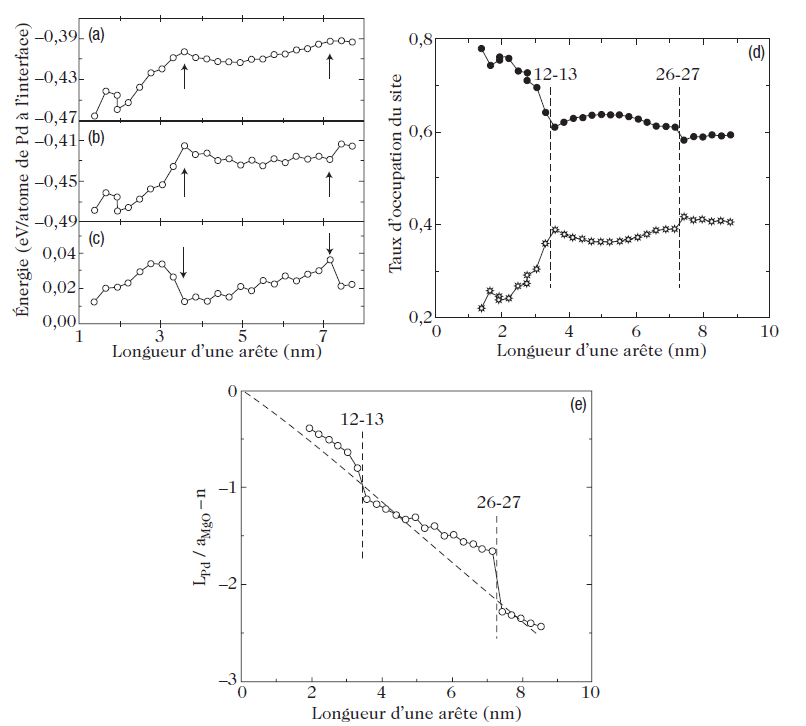
Fig. 3. Adhesion energy (expressed by negative values in the calculation) and occupation of oxygen sites on the surface as a function of the size of the Pd cluster supported on MgO (100). The adhesion energy (a) has two parts: the contribution from Pd–MgO bonds (b) and the contribution from Pd–Pd bonds at the interface (c). The occupation percentage of oxygen sites (black circles) and magnesium sites (stars) is shown in (d). The variation of the epitaxy parameter LPd/aMgO − n between the Pd and MgO lattices at the interfaces is shown in (e). It is equal to zero if all the Pd atoms are above oxygen sites (coherent epitaxy) and decreases linearly (dotted curve) for an incommensurable interface. Taken from Vervisch et al.
Indeed, in the direction parallel to the substrate, the first layer is considerably dilated, whereas the center of the cluster is slightly compressed. The minima of the adhesion energy at 3.5 and 7nm (see Fig. 3a) correspond in fact to minima in the distortion of the crystal lattice due to the appearance of dislocations in the Pd crystal lattice. When dislocations occur, this reduces the elastic stress and the total energy of the system with it, but also the adhesion energy, because the (partial) relaxation of the Pd crystal lattice at the interface causes a drop in the number of Pd–O bonds.
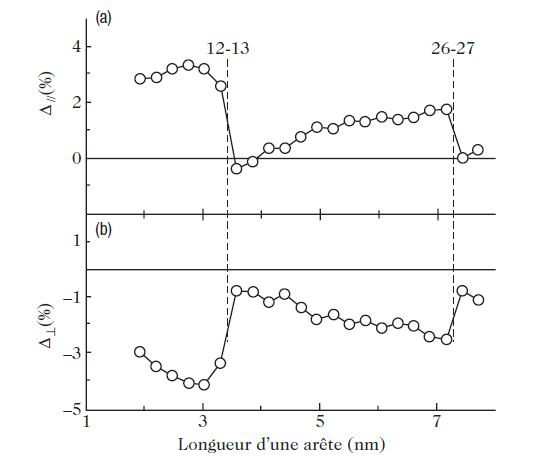
Fig. 4. Average strain in the first Pd layer in contact with the MgO surface (a) parallel and (b) perpendicular to the MgO (100) substrate. Taken from Vervisch et al.
1. P. M¨uller, R. Kern: Surf. Sci. 457, 229 (2000)


|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
في مستشفى الكفيل.. نجاح عملية رفع الانزلاقات الغضروفية لمريض أربعيني
|
|
|