


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 17-3-2021
التاريخ: 3-1-2017
التاريخ: 5-11-2020
التاريخ: 2023-02-04
|
الطاقة المحمولة بالموجات الكهرومغناطيسية
أن الموجات الكهرومغناطيسية تتكون من مجالين متحركين هما الكهربي والمغناطيسي ولما كان هذان المجالان يحتويان على طاقة، لذا فالموجات لابد أن تحمل طاقة عبر الفضاء والموجات الكهرومغناطيسية القادمة من الشمس ، مثلاً، تدفئ الأرض وتمد النباتان بالطاقة اللازمة للنمو. والموجات التي تبثها محطة إرسال تليفزيوني بعيدة، تحمل الطاقة التي توصل الصورة والصوت إلى اجهزة التليفزيون لدينا. دعنا نقوم بحساب مقدار الطاقة المنقولة إلى سطح ما، تسقط عليه موجة كهرومغناطيسية.
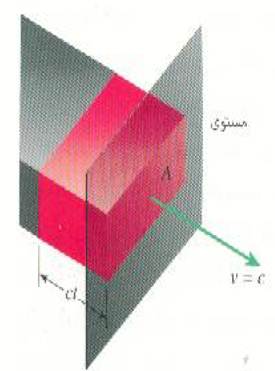
الشكل 1)): يمر حجم مقداره Act من حزمة الموجات عبر المستوى في زمن مقداره t.
أن الطاقة المختزنة في وحدة الحجوم من مجال كهربي مقداره E في الفراغ هي ϵ0E2½. أن الطاقة المختزنة في وحدة الحجوم من مجال مغناطيسي مقداره B هي B2/2μ0 وسننظر في حالة حزمة من الإشعاع الكهرومغناطيسي المبين في الشكل1) ). إن المساحة الطرفية للحزمة هي A وتنتقل إلى اليمين بسرعة الضوء c. وحيث أن الحزمة تنتقل مسافة مقدارها ct خلال الفترة الزمنية t فإن مسافة مقدارها ct من طول الموجي يخترق المستوى في هذه الفترة. ومن ثم يكون حجم الحزمة التي تخترق المستوى في فترة زمنية مقدارها t هو Act وقد أشرنا إلى هذا الحجم بالجزء المظلل في الشكل.
دعنا الآن نختار فترة زمنية قصيرة t بحيث يكون المقدار ct أصغر بكثير من الطول الموجي لإشعاع الحزمة الضوئية، وهكذا يكون كل من E و B ثابتين بالضرورة خلال الحجم المظلل، ونستطيع من ثم كتابة الطاقة المحمولة عبر المستوى بواسطة الحزمة التي حجمها Act لتكون:

ولكي نحسب مقدار الطاقة المارة عبر وحدة المساحات من المستوى وفي وحدة الزمن فما علينا إلا أن نقسم المقدار السابق على t وعلى المساحة A للحزمة. وإذن
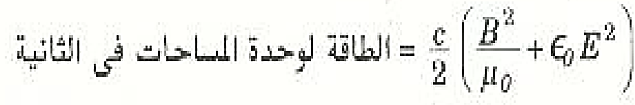
ويطلق على هذا المقدار شدة الموجة I. وبما أن B2= E2/c2= E2ϵ0μ0 فإن المعادلة يمكن كتابتها على الصورة:

وتشير المعادلة الأخيرة إلى أن للحد الخاص بكل من المجالين الكهربي والمغناطيسي نفس المقدار. ونستنتج من ثم أن :
ينقل المجال الكهربي والمجال المغناطيسي في موجة كهرومغناطيسية مقادير متساوية من الطاقة.
إن الشدة التي حسبناها الآن ذات قيمة لحظية لأننا اعتبرنا t كسراً صغيراً جداً من الزمن الدوري للموجة. اما متوسط الشدة عبر كل دورة فهو على درجة أكبر من الأهمية، ولحسابه نحتاج إلى معرفة القيمة المتوسطة للمقدار E2 في دورة واحدة. وقد وجدنا عند دراسة التيارات المترددة أن متوسط مربع أي مقدار يتغير جيبياً هو نصف مربع السعة، أو E2 = ½E20.
( 1أ) 
أو ــ إذ شئنا ــ يمكننا كتابة I بدلالة B0 وهي سعة موجة المجال المغناطيسي، ونذكر أن E = cB ولذا،
(1 ب) 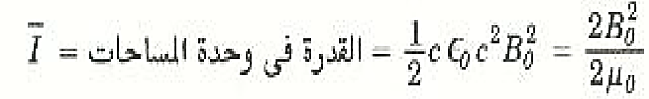
متوسط القدرة المنقولة عبر وحدة المساحات بواسطة موجة كهرومغناطيسية تسقط متعامدة على المساحة هو c ϵ0E20 = cB20/2μ0½ ويسمى هذا المقدار شدة الموجة.
ووحدات SI للشدة هي وات لكل متر مربع (W/m2).



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|