Just 150 years ago, a routine telephone call was not possible, images were delivered in person, and newspapers brought headlines of information that may have been days or weeks old. There was no television or radio coverage of world events. There was no World Wide Web for the world to share its collective knowledge.

Yet today, the ability to communicate with our business partners, colleagues, friends, and loved ones over long distances and at any time of the day is taken for granted. Via phone calls, e-mail, or fax, we transmit pictures, voice or text to almost anyone and anywhere at anytime. Communication has become faster, cheaper, and more commonplace. Mathematics is used to encode, transmit, and decode data in a practical and secure way.

Mathematics drives the new technology and makes the communication revolution possible.

The Challenge of Long-Distance Communication

Communication involves the sharing of ideas, information, sounds, or images. Communicating over distance requires three stages: encoding, transmitting, and decoding. For instance, about 1,500 years ago, the Incas—a highly organized, methodical culture without any written language—used quipus to communicate numeric information. A quipu was a method of encoding numbers for record keeping, and it involved an intricate set of knots tied into colored cotton cords that were connected in specific ways. The knots represented numbers stored in base-10, with the absence of a knot indicating zero, so that the user could distinguish, for example, between 48 and 408. Runners transmitted the information by carrying the quipu from one location to another. Whoever needed to look up the record, studied the knots and decoded the information.

Methods of encoding, transmitting, and decoding have advanced with technology. We now can encode and decode with  binary numbers and transmit via electricity, radio waves, and fiber-optic cables. All of these technologies require mathematics to make them viable.

When considering communication, key questions should be addressed.

1. How does information get encoded and decoded?

2. How can information be transmitted fast enough to make it practical?

3. How can information be sent without data loss or corruption?

4. How can information be sent securely?

The remainder of this article will discuss the first three questions. The answer to the fourth question involves cryptography, a deep and ancient subject with amazing recent mathematical advances whose treatment is beyond the scope of this article. Ironically, it is number theory, the most artistic, pure, abstract, and theoretical branch of mathematics, that provides the method of encryption for sending credit card numbers securely

over the Internet.

The Encoding of Information: Analog versus Digital

There are two models for encoding information. With analog encoding, information is changed continuously from one physical form to another. For example, sound can be encoded into the vibrations of a needle, and stored as scratches on a vinyl disk. A phonograph decodes this information by reversing the process. The disadvantages of analog encoding are noise and inefficiency in the encoding process. Telegraphs, radio, television, cameras,  tape recorders, and telephones were all originally analog inventions. There are now digital versions of all of these.

   With digital encoding, information is transformed into a sequence of numbers. Written language can be encoded by using a specific number for every unique symbol in the language’s alphabet. A picture can be encoded by splitting up the image into tiny pieces and using numbers to represent the color, intensity, and position of each piece. Sound can be encoded by splitting up the soundtrack into small pieces and using numbers to repre-

sent the frequency, intensity, and quality of the sound at each tiny fraction of a second. A similar process can be used with video. Compact disc (CD)

and digital versatile disc (DVD) players are themselves digital devices.

        Compared to analog encoding, digital encoding always misses information. However, if enough samples are taken, the missing pieces of information in between are not discernable. It is like looking outside through a screen door. If the screen is very fine, its presence is barely noticeable, even though it really covers a substantial percentage of one’s view. Of course, if enough samples are not taken, fuzzy pictures, choppy recordings, or missing information may result.

  Binary Numbers and Digital Encoding Physically, it is easier to build transmission devices that send and receive only two different types of signals. Smoke signals and Morse code are early examples of this. Today, electricity can transmit either a high or a low voltage, where high represents 1 and low represents 0. Therefore, information tends to be encoded using only the numbers 0 and 1.

A sequence of digits containing only 0s and 1s is called a binary number. For example, here are the base-10 numbers 0 through 9 represented in binary (in order).

0       1       10       11       100     101       110         111         1000        1001

Using this system, we can show 0 and 1 directly but since there is no symbol for 2, a new column is created that is thought of as the 2s column, writing 2 as 10. Every subsequent number is represented by adding one to the previous number and carrying to new columns whenever necessary. This is like base-10, but we carry when we reach 2 instead of 10. In other words, the columns represent powers of 2 instead of powers of 10, so the columns represent 1, 2, 4, 8 and so on. The binary number 100010011 therefore represents 2⁰+ 2¹+2⁴+ 2⁸  or 1 + 2 + 16 + 256 =275. Every base-10 number can  be encoded into a binary number, and vice versa.

ASCII—The Binary Encoding of Text

How can binary numbers be used to transmit text? ASCII encoding (American Standard Code for Information Interchange, published in 1968, pronounced “askee”) links each character that appears on a keyboard with a unique binary sequence of length eight called a byte. These characters include all upper and lower case letters, digits, various special symbols, and punctuation marks. For example, the ASCII value of “A” is 01000001; the

ASCII value of “B” is 01000010; and the ASCII value of “5” is 00110101.

Each byte consisting of eight binary digits (bits for short) can store 2⁸= 256 different values, which is more than enough to store the various symbols on a keyboard. One bit can store two values, 0 or 1. Two bits can store 00, 01, 10, or 11. With three bits, eight possible sequences can be stored.

With each new bit, the number of possibilities is doubled by adding a 0 in front of all the previous possibilities and by adding a 1. This implies that n bits can store 2n different configurations.

Unicode—The Binary Encoding of Written Characters

ASCII is acceptable for English but falls short when applied to the more diverse worldwide collection of languages and symbols. A more recent advance in written encoding is Unicode. Unicode is a universal, efficient, uniform, and unambiguous way to encode the world’s written languages. It includes symbols for Hebrew, Arabic, and Chinese, as well as hundreds of standard business symbols. Unicode is a new standard that extends ASCII.

 It uses two bytes instead of one, or sixteen bits instead of eight. This gives Unicode the ability to encode a total of 2¹⁶= 65,536 different symbols.

Compression—Huffman Encoding

Compression is a way to shorten messages without losing any information, thereby reducing the size and increasing the transmission speed of the message. The more commonly transmitted letters use shorter sequences while the less commonly transmitted letters use longer sequences.

 Morse code is a form of compression in analog encoding that uses short and long signals to represent letters. We now look at compression for digital encoding of text.

Each character of text is normally encoded with one byte. The inefficiency is that a q is encoded with the same eight bits as a t and yet the two letters occur with a different expected frequency. Huffman encoding takes into account the relative frequencies of the information being encoded.

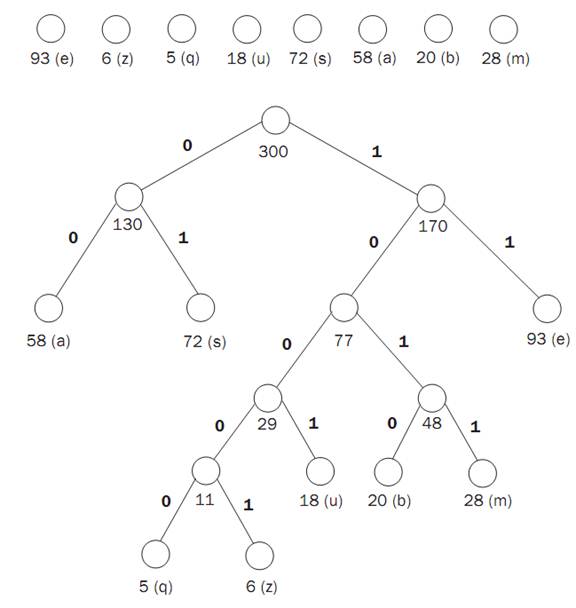
  For example, a message contains 93 e’s, 6 z’s, 5 q’s, 18 u’s, 72 s’s, 58 a’s, 20 b’s and 28 m’s. ASCII encoding requires eight bits per character, or 8 x (93 + 6 + 5 + 18 + 72 + 58 + 20 + 28) = 2,400 bits. Normal flat binary encoding will require three bits per character because there are eight different characters. This gives a total of 3 x (93 + 6+ 5 + 18 + 72 +58+ 20 + 28) = 900 bits.

        Huffman assigns the encoding in the following way: e=11, z =10001,q = 10000, u = 1001, s = 01, a = 00, b =1010, m = 1011. This gives a total message size of (2x 93 + 5 x 6 + 5 x 5+ 4 x 18 + 2x 72 + 2x 58 + 4 x 20 + 4 x 28) = 765, a 15 percent compression. This encoding is done with a “greedy” algorithm that builds a tree in order to determine the optimal encoding. The algorithm starts with a separate single node tree for each character labeled by its frequency. It repeatedly combines the two subtrees with the smallest weights, labeling the new tree with the sum of the labels on the two old trees, until there is just one tree. The initial trees and the final tree are shown below.

Error Correction—Hamming Codes

Error detection and correction allows us to ensure that information is transmitted without loss or corruption. When digital information is transmitted,  it is easy for some of the bits to be corrupted because of lightning storms,  surges in power supply, dirty lenses, and undependable transmission lines.

 How can we make sure that the actual data transmitted are received?

The answer is to add extra bits so that only some of the sequences are legal messages. This increases the size of the message and consequently slows down the transmission time, but allows more accurate transmission. For example, in the case of 4-bit messages, the sender can simply add an extra copy of the four bits making eight bits total. The receiver compares the two copies and requests a retransmission if the two copies differ. For example, the sequence 10001000 is legal but 10001001 would require a retransmission. The downside is that the correct 4-bit message cannot be determined.

Nonetheless, there are strategies that correct errors automatically without any need for retransmission. Assume that the message is broken up into groups of four bits and we want to correct any single bit error in a given group. This time two extra copies of the four bits are added, making the sum twelve bits total. Only sequences of twelve bits with three identical copies of the first four bits are legal. There are 212 possible 12-bit messages and only 24 are legal. If there is a single difference between any two of the three copies, then we know that a single error has occurred and it can be corrected to be the same as the other two identical copies.

  Why three copies? The three copies allow us to pinpoint where the error occurred. The idea is that any two distinct legal messages must differ by at least three bits. Hence an illegal 12-bit message that occurred due to a transmission error of a single bit must have come from a unique original legal message. The decoding is unambiguous. For example, if 100011001000 is received, then the correct message is 100010001000 and there is an error in the sixth bit transmitted.

  What if more than one error occurs? If two or more differences exist, a retransmission can be requested. What if, by chance, many errors occur,  resulting in a nonetheless legal message? That would be undetectable. This scheme was set up to correct only one error per 4-bit sequence. We could correct more than a single error if we were willing to add more redundant information and incur a proportionately larger increase in message and

transmission time.

Hamming Codes.

There is a more efficient way to correct single bit errors, and it is known as Hamming codes. The method is elegant and practical,  but it is also complex. (For an explanation of why it works see Hamming’s book, Coding and Information Theory.) Let 4 + r be the total number of bits sent. Hamming realized that each of the 24 legal message must have 4+ r single-error illegal messages that can be created from it,  and that if any two distinct legal messages must differ by at least three bits, the all of these illegal messages must be mutually distinct. This means that we need at least (4 + r) x 2⁴ distinct illegal messages and 24 distinct legal me sages, totaling (4 + r +1) x 2⁴ distinct messages. Since we have exactl 2^4xr distinct binary sequences, we need 2^4+r = (4 + r + 1)x 2⁴. The reade can check that r must be at least 3.

   Hamming demonstrated how to achieve this lower bound, thereby exhibiting the smallest possible size messages (7) to do single error-correction on 4-bit data messages. Here is how Hamming encoded 4 bits of data into 7 while allowing for the correction of a single error. He wrote his 4 data bits in positions 3, 5, 6, and 7. Then he computed the bits in positions 1, 2 and 4 depending on the number of ones in a particular set of the other positions. These extra bits are called parity bits. He then sets a given parity bit to 0 if the number of 1s in the appropriate positions is even, and to 1 if the number of 1s is odd. The sets of positions for the parity bits in positions 1, 2, and 4 are {3,5,7}, {3,6,7}, and {5,6,7} respectively.

For example, if the message is: 0011, then we have _ _0_111. The {3,5,7} set gives 2 one’s, an even number, so we set position 1 equal to 0. The {3,6,7} set is similar, so position 2 is also 0. The {5,6,7} set has an odd number of 1s so the fourth position is 1. The final encoded 7 bits is: 0001111.

  To decode Hamming’s scheme, the parity bits are recomputed, and if they match what was received, it is a legal message. If they do not match, then the sum of the positions with incorrect parity gives the position of the single-bit error. For example, if 0001111 is corrupted into 0001101, then the parity bit for position 1 is correct, while those for positions 2 and 4 are incorrect. This means that the error is in position 2 + 4 = 6. Hamming codes allow error detection and correction while adding the minimum amount of information to the data.

______________________________________________________________________________________________

Reference

Ascher, Marcia, and Robert Ascher. Mathematics of the Incas: Code of the Quipu. Mineola, NY: Dover Publications, 1997.

Cormen, T. H., C. E. Leiserson, and R. L. Rivest. “Sec. 17.3—Huffman Codes.” In Introduction to Algorithms. New York: McGraw-Hill, 1990.

Hamming, Richard W. Coding and Information Theory, 2nd ed. Englewood Cliffs, NJ: Prentice Hall, 1986.

Katz, Victor J. A History of Mathematics: An Introduction, 2nd ed. Reading, MA: Addison-Wesley, 1998.

Lathi, Bhagwandas P. Modern Digital and Analog Communication Systems, 3rd ed. New York: Oxford University Press, 1998.

Singh, Simon. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. New York: Doubleday, 2000.

Homepage for Unicode. <http://www.unicode.org>.

Details about the life and work of R. Hamming. <http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Hamming.html>.