المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | نسبة المثلثية trigonometric Ratio |
 4325
 01:21 صباحاً
التاريخ: 21-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 352-353|
أقرأ أيضاً
التاريخ: 26-11-2015
1203
التاريخ: 27-12-2015
3706
التاريخ: 8-2-2017
1164
التاريخ: 13-11-2015
2145
|
وجعلها نسب مثلثية ولها في الرياضيات تفسيران هما :
التفسير الأول يرتبط بالمثلث القائم الزاوية حيث النسب المثلثية هي علاقات بين كل اثنين من أضلاع هذا المثلث كما يلي :
التفسير الثاني يرتبط بدائرة الوحدة وكما يلي :
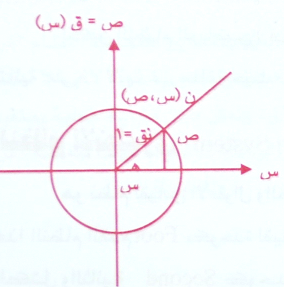
يسمى الاحداثي السيني س ← جيب تمام الزاوية .
وبالرموز س = جتا هـ
ويسمى الاحداثي الصادي ص ← جيب الزاوية
وبالرموز ص = جا هـ
ومن هذا وذلك تنتج بقية النسب المثلثية والتي تسمى هنا بالاقترانات الدائرية من العلاقات التالية :
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
