
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 24-11-2015
التاريخ: 4-1-2016
التاريخ: 29-10-2015
التاريخ: 3-11-2015
|
" يرتبط هذا المنحني بالمستهلك ويحقق له من الأرباح ما يريد "
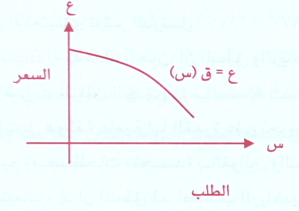
وهو المنحني الذي يبين مقدار تأثر الطلب على سلعة ( س = الكمية ) معينة بسعر تلك السلعة ( ع = السعر) .
فإذا كان الطلب مرناً , فمن الملاحظ أنه ازداد سعر السلعة (ع) قل طلب (س) المستهلك عليها , فالتناسب بين سعر السلعة ومقدار طلبها تناسباً عكسياً لذا فالمنحني يمثل خطاً منحنياً متناقصاً كما في الشكل :



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|