


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 9-1-2017
Date: 11-3-2017
Date: 5-3-2019
|
Some important successes of classical quantum theory
Historical discussions of the developments of quantum theory are dealt with adequately elsewhere, and so we focus only on some key points of classical quantum theory (in which the electron is considered to be a particle). At low temperatures, the radiation emitted by a hot body is mainly of low energy and occurs in the infrared, but as the temperature increases, the radiation becomes successively dull red, bright red and white. Attempts to account for this observation failed until, in 1901, Planck suggested that energy could be absorbed or emitted only in quanta of magnitude ΔE related to the frequency of the radiation, ⱱ, by equation 1.1. The proportionality constant is h, the Planck constant (h =6.626 × 10-34 J s).

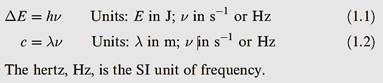
Since the frequency of radiation is related to the wavelength, ⱱ , by equation 1.2, in which c is the speed of light in a vacuum (c = 2.998 x108 ms-1), we can rewrite equation 1.1 in the form of equation 1.3 and relate the energy of radiation to its wavelength.


On the basis of this relationship, Planck derived a relative intensity/wavelength/temperature relationship which was in good agreement with experimental data. This derivation is not straightforward and we shall not reproduce it here.
One of the most important applications of early quantum theory was the interpretation of the atomic spectrum of hydrogen on the basis of the Rutherford–Bohr model of the atom. When an electric discharge is passed through a sample of dihydrogen, the H2 molecules dissociate into atoms, and the electron in a particular excited H atom may be promoted to one of many high energy levels. These states are transient and the electron falls back to a lower energy state, emitting energy as it does so. The consequence is the observation of spectral lines in the emission spectrum of hydrogen; the spectrum (a small part of which is shown in Figure 1.2) consists of groups of discrete lines corresponding to electronic transitions, each of discrete energy. As long ago as 1885, Balmer pointed out that the wavelengths of the spectral lines
observed in the visible region of the atomic spectrum of hydrogen obeyed equation 1.4, in which R is the Rydberg constant for hydrogen, ῡ is the wavenumber in cm-1, and n is an integer 3, 4, 5 . . . This series of spectral lines is known as the Balmer series.
Wavenumber = reciprocal of wavelength; convenient (non- SI) units are ‘reciprocal centimetres’, cm-1 Other series of spectral lines occur in the ultraviolet (Lyman series) and infrared (Paschen, Brackett and Pfund series).
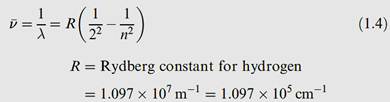
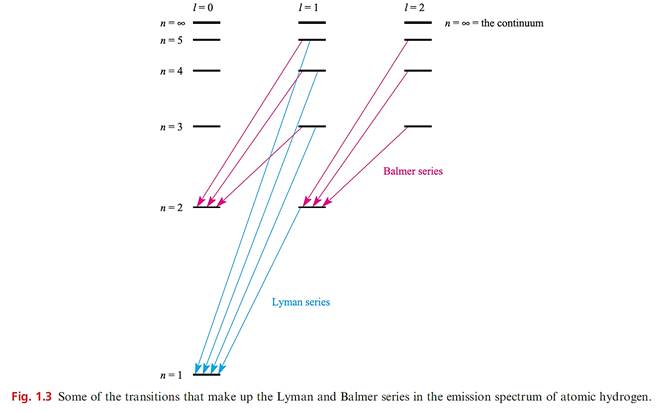
All lines in all the series obey the general expression given in equation 1.5 where n’ > n. For the Lyman series, n = 1, for the Balmer series, n= 2, and for the Paschen, Brackett and Pfund series, n = 3, 4 and 5 respectively. Figure 1.3 shows some of the allowed transitions of the Lyman and Balmer series in the emission spectrum of atomic H. Note the use of the word allowed; the transitions must obey selection rules, to which we return in Section 20.6.





|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|