المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | مشتقات عليا Higher Derivatives |
 2280
 02:11 صباحاً
التاريخ: 14-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 316|
أقرأ أيضاً
التاريخ: 30-3-2019
1868
التاريخ: 23-4-2019
1138
التاريخ: 12-10-2018
2507
التاريخ: 3-11-2021
2731
|
بما ان قَ(س) المشتقة الاولى للاقتران ق(س) وهي بدورها اقتران درجته أقل من درجة ق(س) بواحدة فقط , وكذلك ق=(س) المشتقة الثانية هي اقتران درجة أقل من درجة قَ(س) بواحدة فقط , لذا يمكن استمرار عملية الاشتقاق لإيجاد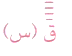 
، 
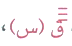حتى ق(ن)(س) المشتقة التونية .
عملية الاشتقاق هذه المستخدمة لإيجاد أي مشتقة من سابقتها تسمى الاشتقاق المتعاقب أو المتتالين مع ملاحظة التسلسل بالاشتقاق والترتيب بدرجات المشتقات إذ لا يمكن إيجاد ق=(س) فالترتيب بالاشتقاق يكون إيجاد قَ(س) ثم ق=(س) ثم 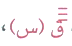حتى ق(ن)(س) ، ونحن لا نحتاج في الرياضيات أكثر من قَ(س) , ق=(س) , 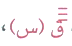فقط والمشتقات العليا تظهر بعد الاشتقاق المتعاقب كما يلي :
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
