المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
معنى قوله تعالى : وَالشُّعَرَاءُ يَتَّبِعُهُمُ الْغَاوُونَ
2025-04-07
معنى قوله تعالى : وَالطَّيْرُ صَافَّاتٍ كُلٌّ قَدْ عَلِمَ صَلاتَهُ وَتَسْبِيحَهُ
2025-04-07
معنى قوله تعالى : وَالْوَزْنُ يَوْمَئِذٍ الْحَقُّ
2025-04-07
معنى قوله تعالى : وَأَنْ أَقِمْ وَجْهَكَ لِلدِّينِ حَنِيفًا
2025-04-07
معنى قوله تعالى : وَإِنَّ اللَّهَ رَبِّي وَرَبُّكُمْ فَاعْبُدُوهُ
2025-04-07
معنى قوله تعالى : وَإِنْ خِفْتُمْ عَيْلَةً
2025-04-07

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
مقومات التنمية الصناعية- المواد الخام
14/9/2022
الاصلاح هدف النهضة الرئيسي
3-04-2015
دفن الميت
13-10-2018
تفسير ظاهرة المد والجزر عند زكريا القزويني
2023-07-11
UNIMAGINABLE POWER
17-9-2020
مـستويـات التنميـة وأهـم مـجالاتـها
5-12-2019


زوايا متبادلة Alternate Angles  
  
6081   01:44 صباحاً   التاريخ: 13-11-2015
المؤلف : صالح رشيد بطارسه
الكتاب أو المصدر : معجم الرياضيات
الجزء والصفحة : 156
القسم : الرياضيات / المثلثات /


أقرأ أيضاً
زوايا متناظرة Corresponding Angles
التاريخ: 13-11-2015 2370
Transforming of degree measure to radian one and back
التاريخ: 12-2-2017 1388
زاوية مركزية Central Angle
التاريخ: 10-11-2015 1677
نسبة المثلثية trigonometric Ratio
التاريخ: 21-12-2015 4713

الزاويتان المتبادلتان هم الزاويتان الواقعتان بين المستقيمين ل1 , ل2 الداخليتين وعلى جهتين من القاطع س ص كما في الشكل .

حيث 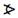1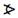 , 2.. بوضع تبادل وإذا كان المستقيمان ل1 , ل2 متوازيين فإن 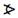1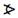 = 2 كونها بوضع تبادل وكذلك 3 = 4 وللتوضيح فإن الزاويتين  المتبادلتان تشكلان حرف Z  وهكذا .

 

 

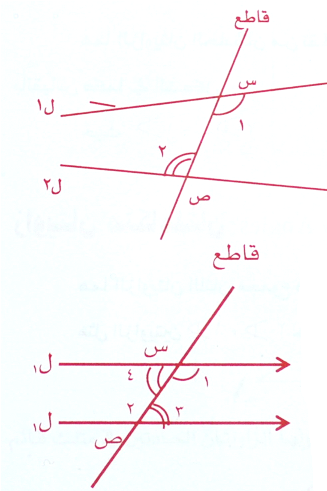
فالزاويتان المتبادلتان متساويتان بالقياس إذا كان المستقيمان ل1 , ل2 متوازين .

 

 

 

 




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
التاريخ / 2025-04-04

الأخبار العلمية
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
التاريخ / 2025-04-04

الساحة الاسلامية
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
التاريخ / 2025-04-07