On generative semantics¹

The basic theory

I would like to discuss some questions having to do with the theory of grammar. I assume that a grammar of a language is a system of rules that relates sounds in the language to their corresponding meanings, and that both phonetic and semantic representations are provided in some language-independent way. I assume that the notion ‘ possible surface structure ’ in a possible natural language is defined in terms of ‘trees’ or ‘phrase-markers’, with the root S, whose node-labels are taken from a finite set of node-labels: S, NP, V,. . .. The notion ‘tree’, or ‘phrase-marker’, is to be defined in one of the usual ways, in terms of predicates like precedes, dominates, and is labeled. Thus a grammar will define an infinite class of surface structures. In addition I assume that a grammar will contain a system of grammatical transformations mapping phrase-markers onto phrase-markers. Each transformation defines a class of well-formed pairs of successive phrase-markers, P_j and P_i+1. These transformations, or well-formedness constraints on successive phrase-markers, P_i and P_j+1, define an infinite class K of finite sequences of phrase-markers, each such sequence P₁, .., P_n meeting the conditions:

(1) (i) P_n is a surface structure

(ii) each pair P_i and P_i+1 meet the well-formedness constraints defined by transformations

(iii) there is no P₀ such that P₀, P₁, ...,P_n meets conditions (i) and (ii).

The members of K are called the syntactic structures generated by the grammar. I will assume that the grammar contains a lexicon, that is, a collection of lexical entries specifying phonological, semantic, and syntactic information. Thus, we assume

(2) a lexical transformation associated with a lexical item I maps a phrase-marker P containing a substructure Q which contains no lexical item into a phrase-marker P' formed by superimposing I over Q.

That is, a lexical transformation is a well-formedness constraint on classes of successive phrase-markers P_i and P_i+1, where P_i is identical to P_i+1 except that where P_i contains a subtree Q, P_i+1 contains the lexical item in question. Various versions of this framework will differ as to where in the grammar lexical transformations apply, whether they apply in a block, etc.

In this sense, transformations, or well-formedness conditions on successive phrase-markers, may be said to perform a ‘filtering function’, in that they ‘filter out ’ derivations containing successive phrase-marker pairs (P_i, P_i+1) which do not meet some well-formedness condition on such pairs. A system of transformations is essentially a filtering device which defines a class of well-formed sequences of phrase-markers by throwing out all of those sequences which contain pairs (P_i, P_i+1) which do not meet some such well-formedness condition, that is, are not related by some transformation. Since transformations define possible derivations only by constraining pairs of successive phrase-markers, I will refer to transformations as ‘local derivational constraints’. A local derivational constraint can be defined as follows. Let ‘ P_i/C₁ ’ mean phrase-marker P_i meets tree-condition C₁. A transformation, or local derivational constraint, is a conjunction of the form P_i/C₁ and P_i+₁/C₂, as where C₁ and C₂ are tree-conditions defining the class of input trees and class of output trees, respectively. It is assumed that:

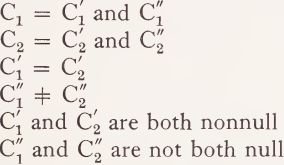
C’₁ (which is identical to C’₂) will be called the structural description (SD) of the transformation. C”₁and C”₂ will be called the structural correlates (SC) of the transformation. The SD of the transformation defines the part of the tree-condition which characterizes both P_i and P_i+1. The SC of the transformation defines the minimal difference between P_i and P_i+1. Thus, a pair (C₁, C₂) defines a local derivational constraint, or ‘ transformation ’. A derivation will be well-formed only if for all i, ɪ ≤ i < n, each pair of phrase-markers (P_i, P_i+1) is well-formed. Such a pair will, in general, be well-formed if it meets some local derivational constraint. There are two sorts of such constraints: optional and obligatory. To say that a local derivational constraint, or transformation, (C_1, C₂) is optional is to say:

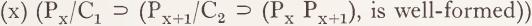
To say that (T_1, T₂) is obligatory is to say:

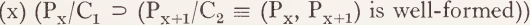
For a derivation to be well-formed it is necessary (but in general not sufficient) for each pair of successive phrase-markers to be well-formed.

In addition to transformations, or local derivational constraints, a grammar will contain certain ‘global derivational contracts’. Rule orderings, for example, are given by global derivational constraints, since they specify where in a given derivation two local derivational constraints can hold relative to one another. Suppose (C₁, C₂) and (C₃, C₄) define local derivational constraints. To say that (C₁, C₂) is ordered before (C₃, C₄) is to state a global derivational constraint of the form:

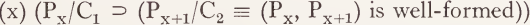
Another example of a global constraint is Ross’coordinate structure constraint which states that if some coordinate node A¹ dominates node A² at some point in the derivatoin P_i, then there can be no P_i+1 such that A² commands A¹ and A¹ does not dominate A², where ‘command’ means ‘belong to a higher clause than’. That is, A commands B if and only if the first S-node higher than A dominates B. This is a global derivational constraint of the form:

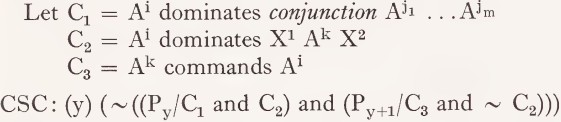
What the coordinate structure constraint does is to keep track of the derivational histories of pairs of nodes Aⁱ and A^k. This is just what elementary transformations and their associated rules of derived constituent structure do: they define constraints on successive phrase-markers, keeping all but one or two nodes constant, and then tell what happens to those one or two other nodes in going from the first tree to the second. It seems reasonable on the basis of our present knowledge to limit individual derivational constraints, both local and global, to tracing the histories of at most two nodes - over a derivation in the case of global constraints, and over two successive trees in the case of local constraints. Other examples of global derivational constraints are Ross’ other constraints on movement rules (Ross [65]), the theory of exceptions (Lakoff [40] and R. Lakoff [44]), Postal’s crossover principle (Postal [57]), output conditions for pronominalization (Lakoff [41]), etc. It should be clear that all theories of transformational grammar have included both local and global derivational constraints. The question arises as to what kinds of local and global derivational constraints exist in natural languages. I will suggest that there is a wider variety than had previously been envisioned. It is assumed that derivational constraints will be restricted to hold either at particular levels in a derivation (semantic representation, surface structure, shallow structure, and deep structure if such exists), or to range over entire derivations or parts of derivations occurring between levels. Constraints holding at particular levels define well-formedness conditions for those levels, and so are analogous to McCawley’s node-acceptability conditions [47], which play the role of phrase-structure rules in a theory containing deep structures.

Given a syntactic structure (P₁, . . ., P_n) we define the semantic representation SR of a sentence as SR = (P₁, PR, Top, F,. . .), where PR is a conjunction of presuppositions, Top is an indication of the ‘topic’ of the sentence, and F is the indication of the focus of the sentence.² We leave open the question of whether there are other elements of semantic representation that need to be accounted for.

Perhaps some examples are in order. Let us start with presuppositions.³ Pedro regretted being Norwegian presupposes thet Pedro is Norwegian. Sam’s murderer reads Reader’s Digest presupposes that Sam was murdered. In general, a sentence may be either true or false only if all its presuppositions are true. Since any proposition (at least nonperformative ones) may be presupposed, it is assumed that the elements of PR are of the same form as those of P₁, and that they are defined by the same well-formedness conditions. The notation given above, with PR as a member of an ordered n-tuple, assumes that presuppositions are structurally independent of P₁. However, Morgan, in an important paper [52], has argued convincingly that there are cases where presuppositions must be linked to certain propositions embedded in P₁ and that such links are identical to, or share properties with, conjunctions. He has also shown that presuppositions may be attributed not merely to the speaker and addressee, but also to the subjects of certain predicates in P₁ (e.g., verbs of saying, thinking, dreaming, etc.). For example, know is factive, and presupposes the truth of its complement. Everyone knows that I am a Martian presupposes that I am a Martian. Dream on the other hand is counterfactual, and presupposes the falsehood of its complement. I dreamt that I was a Martian presupposes that I’m not a Martian. Morgan has noticed sentences like: I dreamt that I was a Martian and that everyone knew that I was a Martian. If presuppositions were unstructured relative to P₁, this sentence would contain contradictory presuppositions, since dream presupposes that I’m not a Martian and know presupposes that I am a Martian. Morgan takes this to show that presuppositions cannot be unstructured relative to P₁; rather they must be associated with certain verbs in P₁.

Since know is embedded in the complement of dream, the presupposition of know is only assumed to be true of the world of my dream. However, the presupposition of dream is assumed to be true of the world of the speaker. There is no contradiction since the presuppositions are true of different possible worlds. The notation given above, which represents the traditional position that presuppositions are unstructured with respect to nonpresupposed elements of meaning, would appear to be false on the basis of Morgan’s argument. However, we will keep the above notation throughout the remainder of this work, since the consequences of Morgan’s observations are not well understood at present and since his examples are not directly relevant to the subsequent discussion.⁴

The notion of ‘ topic ’ is an ancient one in the history of grammatical investigation. Grammarians have long recognized that sentences have special devices for indicating what is under discussion. Preposing of topics is common. For example, in John, Mary hates him, John is the topic, while in Mary, she hates John, Mary is the topic. Clearly, an adequate account of semantic representation must take account of this notion. As with presuppositions, it is usually assumed that topics are structurally independent of the other components of meaning, as our notation indicates. As we will discuss below, this may well not be the case. However, throughout what follows, we will assume the traditional position in an attempt to minimize controversy.

‘Focus’ is another traditional notion in grammar. Halliday [24] describes the information focus as the constituent containing new, rather than assumed information. The information focus often has heavy stress. Thus, in JOHN washed the car yesterday, the speaker is assuming that the car was washed yesterday and telling the addressee that the person who did it was John. Again, it is usually assumed that the semantic content of the ‘focus’ is structurally independent of other components of meaning. Our notation reflects this traditional position, although, as in the case of topic and presupposition, nothing that we have to say depends crucially on the correctness of this position.

I will refer to the above theory of grammar as a ‘basic theory’, simply for convenience and with no intention of suggesting that there is anything ontologically, psychologically, or conceptually ‘basic’ about this theory. Most of the work in generative semantics since 1967 has assumed the framework of the basic theory. It should be noted that the basic theory permits a variety of options that were assumed to be unavailable in previous theories. For example, it is not assumed that lexical insertion transformations apply in a block, with no intervening nonlexical trans¬ formations. The option that lexical and nonlexical transformations may be interspersed is left open.

As should be obvious from the above discussion, the basic theory does not assume any notion of ‘ directionality of mapping ’ from phonetics to semantics or semantics to phonetics.⁵ Some writers on transformational grammar have, however, used locutions that might mislead readers into believing that they assume some notion of directionality. For example, Chomsky [10] remarks that ‘properties of surface structure play a distinctive role in semantic interpretation However, as Chomsky points out a number of times in that work, the notion of directionality in a derivation is meaningless, so that Chomsky’s locution must be taken as having the same significance as ‘ Semantic representation plays a distinctive role in determining properties of surface structure’ and nothing more. Both statements would have exactly as much significance as the more neutral locution ‘ Semantic representation and surface structure are related by a system of rules’. The basic theory allows for a notion of transformational cycle in the sense of Aspects, so that a sequence of cyclical rules applies ‘from the bottom up’, first to the lowermost S’s, then to the next highest, etc. We assume that the cyclical transformations start applying with P_k and finish applying (to the highest S) at P₁ where k is less than ɪ. We will say in this case that the cycle applies ‘upward toward the surface structure’ (though, of course, we could just as well say that it applies ‘ downward toward the semantic representation’, since directionality has no significance).

It should be noted that a transformational cycle defines an ‘orientation’ on a derivation, and readers should be cautioned from confusing the notion ‘cyclical orientation of a derivation’ with the notion ‘directionality of a derivation’. The former is a real and quite important notion; the latter is meaningless. To say that a cycle is oriented ‘ upward-toward-the-surface ’ is the same as to say that it is oriented ‘ downward-toward-the-semantics’, and such terminology makes no claim about where a derivation ‘begins’. Most theories of transformational grammar that have been seriously entertained have assumed a cyclical orientation that is upward-toward-the-surface. However, it is possible to envision a theory with an upward-toward-the-semantics cyclic orientation. Moreover, it is possible to imagine theories with more than one cyclic orientation. Consider a sequence of phrase-markers P₁ . . ., P_i, . . ., P_n. One could imagine a theory such that P₁ . . ., P_i had an upward-towards-the-semantics cyclic orientation and P_i, . . ., P_n had an upward-toward-the-surface orientation, or vice versa.

The basic theory does not necessarily include a level of ‘deep structure’, and the question as to whether such a level exists is an empirical question in the basic theory. We assume that the notion of ‘deep structure’ is defined in the following way. (i) Assume that all lexical insertion rules apply in a block, (ii) Assume that all upwards-toward-the-surface cyclic rules follow all lexical insertion rules. We define the output of the last lexical insertion rule as ‘ deep structure ’.

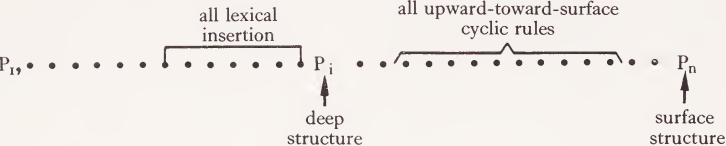
I will discuss an example of a global derivational constraint and the evidence it provides for the question of whether ‘ deep structure ’ in this sense exists.

¹ Generative semantics is an outgrowth of transformational grammar as developed by Harris, Chomsky, Lees, Klima, Postal, and others. The generative semantics position was arrived at through an attempt on the part of such linguists as Postal, Fillmore, Ross, McCawley, Bach, R. Lakoff, Perlmutter, myself, and others to apply consistently the methodology of transformational grammar to an ever-increasing body of data. We have not all reached the same conclusions, and those presented here are only my own. However, I think it is fair to say that there has developed in recent years a general consensus in this group that semantics plays a central role in syntax. The generative semantics position is, in essence, that syntax and semantics cannot be separated and that the role of transformations, and of derivational constraints in general, is to relate semantic representations and surface structures. As in the case of generative grammar, the term ‘generative’ should be taken to mean ‘complete and precise’.

An earlier version of part of this paper has appeared in Binnick et al. [4]. The present paper is an early draft of some chapters of a book in progress to be called Generative Semantics [43]. I would like to thank R. T. Lakoff, J. D. McCawley, D. M. Perlmutter, P. M. Postal, and J. R. Ross for lengthy and informative discussions out of which most of the material discussed here developed. I would also like to thank Drs McCawley, Postal, and Ross for reading an earlier draft of this manuscript and suggesting many improvements. Any mistakes are, of course, my own. I would also like to take this opportunity to express my gratitude to Professor Susumu Kuno of Harvard University, who has done much over the past several years to make my research possible. The work was supported in part by grant GS-1934 from the National Science Foundation to Harvard University.

² It seems possible to eliminate coordinates for topic and focus in favor of appropriate representations in the presuppositional part of the sentence. Thus, it is conceivable that semantic representations can be limited to ordered pairs (P₁, PR). Such ordered pairs can equivalently be viewed as two-place relationships between the phrase-markers involved. Thus, we might represent (P₁, PR) as P₁ ----> PR, where ‘---->’ is to be read as ‘presupposes’, and where PR is drawn from the class of possible P₁’s. Under this interpretation, ‘----->’ can be viewed either as a relation between two parts of a single semantic representation or as a relation between two different semantic representations. Under the latter view, derivational constraints would become transderivational constraints, constraints holding across derivations. It seems to me to be an open question as to whether the theory of grammar needs to be extended to encompass such transderivational constraints. We will assume in the remainder of this paper that it does not. However, it is at least conceivable that transderivational constraints will be necessary and that semantic representations can be limited to P₁’s with presuppositional information given transderivationally.

³ I have used the term presupposition for what some philosophers might prefer to call ‘pragmatic implication’. I assume that presuppositions are relative to speakers (and sometimes addressees and other persons mentioned in the sentence). Consider the example given in the text: Pedro regretted being Norwegian. A speaker cannot be committed to either the truth or falsity of this sentence without being committed to the truth of Pedro was Norwegian. The sentence Pedro regretted being Norwegian, although I know that he wasn’t is contradictory. When I say that a given sentence presupposes a second sentence, I will mean that a speaker, uttering and committing himself to the truth of the first sentence will be committing himself to the truth of the second sentence.

⁴ Assuming ‘----->’ to indicate the relation ‘presupposes’, we might represent embedded presuppositions as follows:

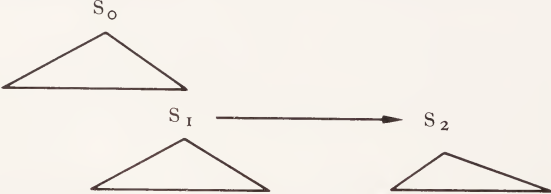
Here the embedded S₁ would be presupposing S₂. In many Cases, like those discussed above, it will not be the case that S₀ will also presuppose S₂.

⁵ Some readers may have received an incorrect impression of the basic theory with regard to this issue from the confusing discussion of directionality by Chomsky [10]. Chomsky does not claim in that article that any advocates of the basic theory have ever said that directionality matters in any way. However, Chomsky’s odd use of quotation marks and technical terms in that paper has led some readers to believe that he had made such a mistaken claim. A close reading of Chomsky’s paper should clarify matters. On page 196, Chomsky says: ‘let us consider once again the problem of constructing a “semantically based” theory of generative grammar that is a genuine alternative to the standard theory.’ He then outlines a theory, in example (32), containing S (a semantic representation) and P (a phonetic representation), and he correctly notes that it makes no sense to speak of the ‘direction’ of a derivation from S to P or P to S. He concludes, on the same page: ‘Consequently, it is senseless to propose as an alternative to (32) a “semantically based” conception of grammar in which S is “selected first” and then mapped onto the surface structure Pn and ultimately P.’ Here he gives ‘directionality’ as the defining characteristic of what he calls a “‘semantically based” theory of grammar’. His next two sentences are: ‘ Consider once again a theory such as that proposed by McCawley in which Px is identified with S and condition (3) is dropped so that “deep structure” is undefined. Let us consider again how we might proceed to differentiate this formulation - let us call it “semantically based grammar” — from the standard theory.’

Having first used ‘“semantically-based” theory of grammar’ as a technical term for the ‘directionality’ position, he then uses “‘semantically based grammar”’ as a new technical term to describe McCawley’s position. Of course, McCawley has never advocated the ‘ directionality ’ position and Chomsky has not said that he has. But one can see how such a bewildering use of technical terms might lead readers to such a mistaken conclusion. The only person that Chomsky cites as being a supporter of the ‘directionality’ position is Chafe [7], who has never been an advocate of the basic theory. However, Chomsky does not cite any page references, and in reading through Chafe’s paper, I have been unable to find any claim to the effect that directionality has empirical consequences.