المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | زاوية المرجع Reference Angle |
 15139
 02:28 صباحاً
التاريخ: 10-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 152|
أقرأ أيضاً
التاريخ: 10-11-2015
1967
التاريخ: 9-2-2017
1371
التاريخ: 12-2-2017
1394
التاريخ: 12-2-2017
1561
|
وتسمى الزاوية الأساسية أو الأصلية . وهي اصغر زاوية حادة هــ حيث <هـ<90 موجبة تنحصر بين محور السينات وضلع انتهاء الزاوية الذي يقطع محيط الدائرة الوحدة في الربع الأول كما في الشكل .
ويستفاد منها في إيجاد النسب المثلثية للزوايا غير الحادة ل حيث 90<ك<360
كما يلي : عندما ك = 120
|
|
|
|
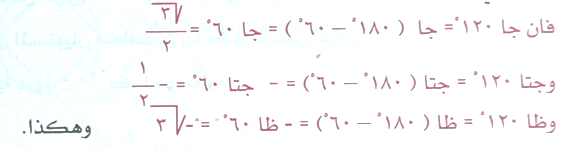
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|
