Now we must analyze our engines. One thing is clear: we will lose something if the engines contain devices in which there is friction. The best engine will be a frictionless engine. We assume, then, the same idealization that we did when we studied the conservation of energy; that is, a perfectly frictionless engine.

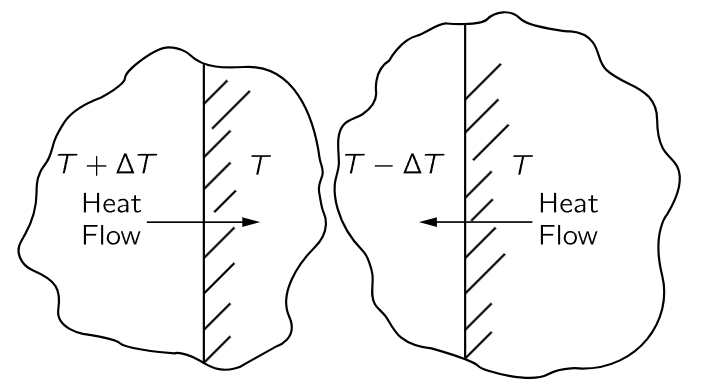
Fig. 44–4. Reversible heat transfer.

We must also consider the analog of frictionless motion, “frictionless” heat transfer. If we put a hot object at a high temperature against a cold object, so that the heat flows, then it is not possible to make that heat flow in a reverse direction by a very small change in the temperature of either object. But when we have a practically frictionless machine, if we push it with a little force one way, it goes that way, and if we push it with a little force the other way, it goes the other way. We need to find the analog of frictionless motion: heat transfer whose direction we can reverse with only a tiny change. If the difference in temperature is finite, that is impossible, but if one makes sure that heat flows always between two things at essentially the same temperature, with just an infinitesimal difference to make it flow in the desired direction, the flow is said to be reversible (Fig. 44–4). If we heat the object on the left a little, heat will flow to the right; if we cool it a little, heat will flow to the left. So we find that the ideal engine is a so-called reversible engine, in which every process is reversible in the sense that, by minor changes, infinitesimal changes, we can make the engine go in the opposite direction. That means that nowhere in the machine must there be any appreciable friction, and nowhere in the machine must there be any place where the heat of the reservoirs, or the flame of the boiler, is in direct contact with something definitely cooler or warmer.

Fig. 44–5. Steps in Carnot cycle.

Let us now consider an idealized engine in which all the processes are reversible. To show that such a thing is possible in principle, we will give an example of an engine cycle which may or may not be practical, but which is at least reversible, in the sense of Carnot’s idea. Suppose that we have a gas in a cylinder equipped with a frictionless piston. The gas is not necessarily a perfect gas. The fluid does not even have to be a gas, but to be specific let us say we do have a perfect gas. Also, suppose that we have two heat pads, T₁ and T₂—great big things that have definite temperatures, T₁ and T₂. We will suppose in this case that T₁ is higher than T₂. Let us first heat the gas and at the same time expand it, while it is in contact with the heat pad at T₁. As we do this, pulling the piston out very slowly as the heat flows into the gas, we will make sure that the temperature of the gas never gets very far from T₁. If we pull the piston out too fast, the temperature of the gas will fall too much below T₁ and then the process will not be quite reversible, but if we pull it out slowly enough, the temperature of the gas will never depart much from T₁. On the other hand, if we push the piston back slowly, the temperature would be only infinitesimally higher than T₁, and the heat would pour back. We see that such an isothermal (constant-temperature) expansion, done slowly and gently enough, is a reversible process.

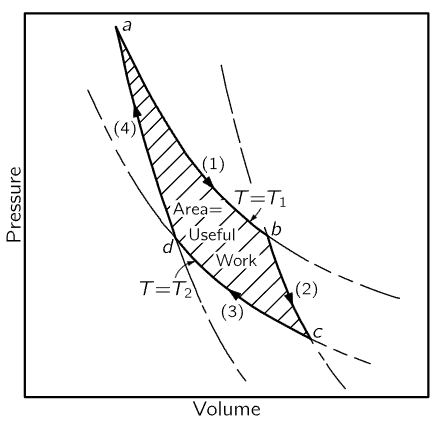
Fig. 44–6. The Carnot cycle.

To understand what we are doing, we shall use a plot (Fig. 44–6) of the pressure of the gas against its volume. As the gas expands, the pressure falls. The curve marked (1) tells us how the pressure and volume change if the temperature is kept fixed at the value T₁. For an ideal gas this curve would be PV=NkT₁. During an isothermal expansion the pressure falls as the volume increases until we stop at the point b. At the same time, a certain heat Q₁ must flow into the gas from the reservoir, for if the gas were expanded without being in contact with the reservoir it would cool off, as we already know. Having completed the isothermal expansion, stopping at the point b, let us take the cylinder away from the reservoir and continue the expansion. This time we permit no heat to enter the cylinder. Again we perform the expansion slowly, so there is no reason why we cannot reverse it, and we again assume there is no friction. The gas continues to expand and the temperature falls, since there is no longer any heat entering the cylinder.

We let the gas expand, following the curve marked (2), until the temperature falls to T₂, at the point marked c. This kind of expansion, made without adding heat, is called an adiabatic expansion. For an ideal gas, we already know that curve (2) has the form PV^γ=constant, where γ is a constant greater than 1, so that the adiabatic curve has a more negative slope than the isothermal curve. The gas cylinder has now reached the temperature T₂, so that if we put it on the heat pad at temperature T₂ there will be no irreversible changes. Now we slowly compress the gas while it is in contact with the reservoir at T₂, following the curve marked (3) (Fig. 44–5, Step 3). Because the cylinder is in contact with the reservoir, the temperature does not rise, but heat Q₂ flows from the cylinder into the reservoir at the temperature T₂. Having compressed the gas isothermally along curve (3) to the point d, we remove the cylinder from the heat pad at temperature T₂ and compress it still further, without letting any heat flow out. The temperature will rise, and the pressure will follow the curve marked (4). If we carry out each step properly, we can return to the point a at temperature T₁ where we started, and repeat the cycle.

We see that on this diagram we have carried the gas around a complete cycle, and during one cycle we have put Q₁ in at temperature T₁, and have removed Q₂ at temperature T₂. Now the point is that this cycle is reversible, so that we could represent all the steps the other way around. We could have gone backwards instead of forwards: we could have started at point a, at temperature T₁, expanded along the curve (4), expanded further at the temperature T₂, absorbing heat Q₂, and so on, going around the cycle backward. If we go around the cycle in one direction, we must do work on the gas; if we go in the other direction, the gas does work on us.

Incidentally, it is easy to find out what the total amount of work is, because the work during any expansion is the pressure times the change in volume, ∫PdV. On this particular diagram, we have plotted P vertically and V horizontally. So if we call the vertical distance y and the horizontal distance x, this is ∫ydx—in other words, the area under the curve. So the area under each of the numbered curves is a measure of the work done by or on the gas in the corresponding step. It is easy to see that the net work done is the shaded area of the picture.

Fig. 44–7. Reversible engine A being driven backwards by engine B.

Now that we have given a single example of a reversible machine, we shall suppose that other such engines are also possible. Let us assume that we have a reversible engine A which takes Q₁ at T₁, does work W, and delivers some heat at T₂. Now let us assume we have any other engine B, made by man, already designed or not yet invented, made of rubber bands, steam, or whatever, reversible or not, which is designed so that it takes in the same amount of heat Q₁ at T₁, and rejects the heat at the lower temperature T₂ (Fig. 44–7). Assume that engine B does some work, W′. Now we shall show that W′ is not greater than W—that no engine can do more work than a reversible one. Why? Suppose that, indeed, W′ were bigger than W. Then we could take the heat Q₁ out of the reservoir at T₁, and with engine B we could do work W′ and deliver some heat to the reservoir at T₂; we do not care how much. That done, we could save some of the work W′, which is supposed to be greater than W; we could use a part of it, W, and save the remainder, W′−W, for useful work. With the work W we could run engine A backwards because it is a reversible engine. It will absorb some heat from the reservoir at T₂ and deliver Q₁ back to the reservoir at T₁. After this double cycle, the net result would be that we would have put everything back the way it was before, and we would have done some excess work, namely W′−W, and all we would have done would be to extract energy from the reservoir at T₂! We were careful to restore the heat Q₁ to the reservoir at T₁. So that reservoir can be small and “inside” our combined machine A+B, whose net effect is therefore to extract a net heat W′−W from the reservoir at T₂ and convert it into work. But to obtain useful work from a reservoir at a single temperature with no other changes is impossible according to Carnot’s postulate; it cannot be done. Therefore, no engine which absorbs a given amount of heat from a higher temperature T₁ and delivers it at the temperature T₂ can do more work than a reversible engine operating under the same temperature conditions.

Now suppose that engine B is also reversible. Then, of course, not only must W′ be not greater than W, but now we can reverse the argument and show that W cannot be greater than W′. So, if both engines are reversible they must both do the same amount of work, and we thus come to Carnot’s brilliant conclusion: that if an engine is reversible, it makes no difference how it is designed, because the amount of work one will obtain if the engine absorbs a given amount of heat at temperature T₁ and delivers heat at some other temperature T₂ does not depend on the design of the engine. It is a property of the world, not a property of a particular engine.

If we could find out what the law is that determines how much work we obtain when we absorb the heat Q₁ at T₁ and deliver heat at T₂, this quantity would be a universal thing, independent of the substance. Of course if we knew the properties of a particular substance, we could work it out and then say that all other substances must give the same amount of work in a reversible engine. That is the key idea, the clue by which we can find the relationship between how much, for instance, a rubber band contracts when we heat it, and how much it cools when we let it contract. Imagine that we put that rubber band in a reversible machine, and that we make it go around a reversible cycle. The net result, the total amount of work done, is that universal function, that great function which is independent of substance. So we see that a substance’s properties must be limited in a certain way; one cannot make up anything he wants, or he would be able to invent a substance which he could use to produce more than the maximum allowable work when he carried it around a reversible cycle. This principle, this limitation, is the only real rule that comes out of the thermodynamics.