Now we go on to consider a still more advanced and interesting proposition that is as follows. Suppose we have a charged oscillator like those we were talking about when we were discussing light, let us say an electron oscillating up and down in an atom. If it oscillates up and down, it radiates light. Now suppose that this oscillator is in a very thin gas of other atoms, and that from time to time the atoms collide with it. Then in equilibrium, after a long time, this oscillator will pick up energy such that its kinetic energy of oscillation is 1/2 kT, and since it is a harmonic oscillator, its entire energy will become kT. That is, of course, a wrong description so far, because the oscillator carries electric charge, and if it has an energy kT it is shaking up and down and radiating light. Therefore, it is impossible to have equilibrium of real matter alone without the charges in it emitting light, and as light is emitted, energy flows away, the oscillator loses its kT as time goes on, and thus the whole gas which is colliding with the oscillator gradually cools off. And that is, of course, the way a warm stove cools, by radiating the light into the sky, because the atoms are jiggling their charge and they continually radiate, and slowly, because of this radiation, the jiggling motion slows down.

On the other hand, if we enclose the whole thing in a box so that the light does not go away to infinity, then we can eventually get thermal equilibrium. We may either put the gas in a box where we can say that there are other radiators in the box walls sending light back or, to take a nicer example, we may suppose the box has mirror walls. It is easier to think about that case. Thus we assume that all the radiation that goes out from the oscillator keeps running around in the box. Then, of course, it is true that the oscillator starts to radiate, but pretty soon it can maintain its kT of energy in spite of the fact that it is radiating, because it is being illuminated, we may say, by its own light reflected from the walls of the box. That is, after a while there is a great deal of light rushing around in the box, and although the oscillator is radiating some, the light comes back and returns some of the energy that was radiated.

We shall now determine how much light there must be in such a box at temperature T in order that the shining of the light on this oscillator will generate just enough energy to account for the light it radiated.

Let the gas atoms be very few and far between, so that we have an ideal oscillator with no resistance except radiation resistance. Then we consider that at thermal equilibrium the oscillator is doing two things at the same time. First, it has a mean energy kT, and we calculate how much radiation it emits. Second, this radiation should be exactly the amount that would result because of the fact that the light shining on the oscillator is scattered. Since there is nowhere else the energy can go, this effective radiation is really just scattered light from the light that is in there.

Thus we first calculate the energy that is radiated by the oscillator per second, if the oscillator has a certain energy. The energy radiated per radian divided by the energy of the oscillator is called 1/Q: 1/Q=(dW/dt)/ω₀W. Using the quantity γ, the damping constant, this can also be written as 1/Q=γ/ω₀, where ω₀ is the natural frequency of the oscillator—if gamma is very small, Q is very large. The energy radiated per second is then

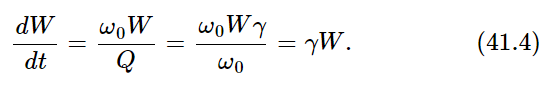
The energy radiated per second is thus simply gamma times the energy of the oscillator. Now the oscillator should have an average energy kT, so we see that gamma kT is the average amount of energy radiated per second:

Now we only have to know what gamma is. It is

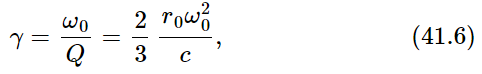
where r₀=e²/mc² is the classical electron radius, and we have set λ=2πc/ω₀.

Our final result for the average rate of radiation of light near the frequency ω₀ is therefore

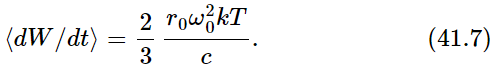
Next we ask how much light must be shining on the oscillator. It must be enough that the energy absorbed from the light (and thereupon scattered) is just exactly this much. In other words, the emitted light is accounted for as scattered light from the light that is shining on the oscillator in the cavity. So we must now calculate how much light is scattered from the oscillator if there is a certain amount—unknown—of radiation incident on it. Let I(ω)dω be the amount of light energy there is at the frequency ω, within a certain range dω (because there is no light at exactly a certain frequency; it is spread all over the spectrum). So I(ω) is a certain spectral distribution which we are now going to find—it is the color of a furnace at temperature T that we see when we open the door and look in the hole. Now how much light is absorbed? We worked out the amount of radiation absorbed from a given incident light beam, and we calculated it in terms of a cross section. It is just as though we said that all of the light that falls on a certain cross section is absorbed. So the total amount that is re-radiated (scattered) is the incident intensity I(ω)dω multiplied by the cross section σ.

The formula for the cross section did not have the damping included. It is not hard to go through the derivation again and put in the resistance term, which we neglected. If we do that, and calculate the cross section the same way, we get

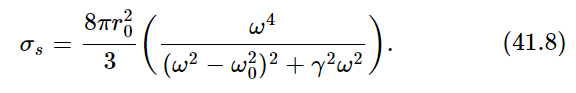
Now, as a function of frequency, σ_s is of significant size only for ω very near to the natural frequency ω₀. (Remember that the Q for a radiating oscillator is about 10⁸.) The oscillator scatters very strongly when ω is equal to ω₀, and very weakly for other values of ω. Therefore, we can replace ω by ω₀ and ω²−ω²₀ by 2ω₀(ω−ω₀), and we get

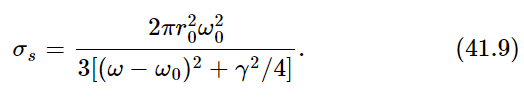
Now the whole curve is localized near ω=ω₀. (We do not really have to make any approximations, but it is much easier to do the integrals if we simplify the equation a bit.) Now we multiply the intensity in a given frequency range by the cross section of scattering, to get the amount of energy scattered in the range dω. The total energy scattered is then the integral of this for all ω. Thus

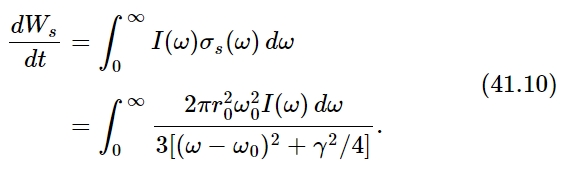
Now we set dW_s/dt=3γkT. Why three? Because when we made our analysis of the cross section in Chapter 32, we assumed that the polarization was such that the light could drive the oscillator. If we had used an oscillator which could move only in one direction, and the light, say, was polarized in the wrong way, it would not give any scattering. So we must either average the cross section of an oscillator which can go only in one direction, over all directions of incidence and polarization of the light or, more easily, we can imagine an oscillator which will follow the field no matter which way the field is pointing. Such an oscillator, which can oscillate equally in three directions, would have 3kT average energy because there are 3 degrees of freedom in that oscillator. So we should use 3γkT because of the 3 degrees of freedom.

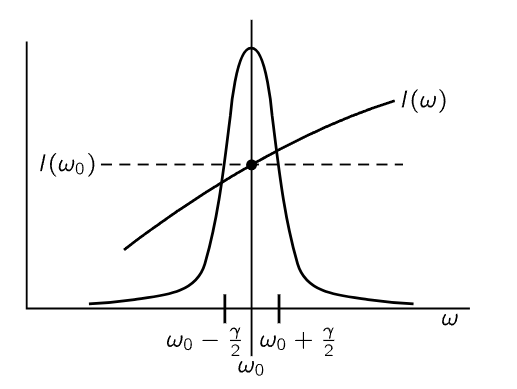
Fig. 41–3. The factors in the integrand (41.10). The peak is the resonance curve 1/[(ω−ω₀)²+γ²/4]. To a good approximation the factor I(ω) can be replaced by I(ω₀).

Now we have to do the integral. Let us suppose that the unknown spectral distribution I(ω) of the light is a smooth curve and does not vary very much across the very narrow frequency region where σ_s is peaked (Fig. 41–3). Then the only significant contribution comes when ω is very close to ω₀, within an amount gamma, which is very small. So therefore, although I(ω) may be an unknown and complicated function, the only place where it is important is near ω=ω₀, and there we may replace the smooth curve by a flat one—a “constant”—at the same height. In other words, we simply take I(ω) outside the integral sign and call it I(ω₀). We may also take the rest of the constants out in front of the integral, and what we have left is

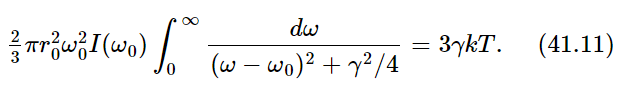
Now, the integral should go from 0 to ∞, but 0 is so far from ω₀ that the curve is all finished by that time, so we go instead to minus ∞—it makes no difference and it is much easier to do the integral. The integral is an inverse tangent function of the form ∫dx/(x²+a²). If we look it up in a book, we see that it is equal to π/a. So what it comes to for our case is 2π/γ. Therefore, we get, with some rearranging,

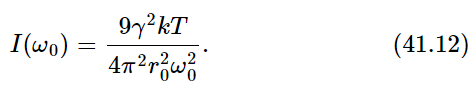
Then we substitute the formula (41.6) for gamma (do not worry about writing ω₀; since it is true of any ω₀, we may just call it ω) and the formula for I(ω) then comes out

And that gives us the distribution of light in a hot furnace. It is called the blackbody radiation. Black, because the hole in the furnace that we look at is black when the temperature is zero.

Inside a closed box at temperature T, (41.13) is the distribution of energy of the radiation, according to classical theory. First, let us notice a remarkable feature of that expression. The charge of the oscillator, the mass of the oscillator, all properties specific to the oscillator, cancel out, because once we have reached equilibrium with one oscillator, we must be at equilibrium with any other oscillator of a different mass, or we will be in trouble. So this is an important kind of check on the proposition that equilibrium does not depend on what we are in equilibrium with, but only on the temperature. Now let us draw a picture of the I(ω) curve (Fig. 41–4). It tells us how much light we have at different frequencies.

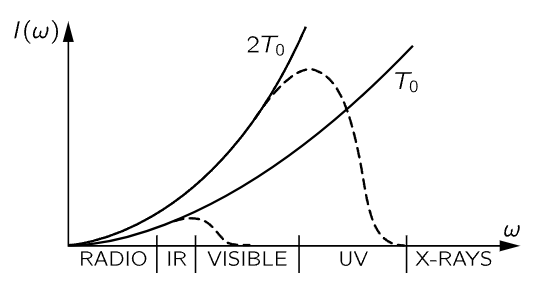
Fig. 41–4. The blackbody intensity distribution at two temperatures, according to classical physics (solid curves). The dashed curves show the actual distribution.

The amount of intensity that there is in our box, per unit frequency range, goes, as we see, as the square of the frequency, which means that if we have a box at any temperature at all, and if we look at the x-rays that are coming out, there will be a lot of them!

Of course we know this is false. When we open the furnace and take a look at it, we do not burn our eyes out from x-rays at all. It is completely false. Furthermore, the total energy in the box, the total of all this intensity summed over all frequencies, would be the area under this infinite curve. Therefore, something is fundamentally, powerfully, and absolutely wrong.

Thus was the classical theory absolutely incapable of correctly describing the distribution of light from a blackbody, just as it was incapable of correctly describing the specific heats of gases. Physicists went back and forth over this derivation from many different points of view, and there is no escape. This is the prediction of classical physics. Equation (41.13) is called Rayleigh’s law, and it is the prediction of classical physics, and is obviously absurd.