


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-03-16
التاريخ: 28-12-2019
التاريخ: 2024-04-06
التاريخ: 2023-03-30
|
We now have to ask: Is the field Ea the kind we would expect from oscillating charges in the plate? If we can show that it is, we will then have calculated what the index n should be! [Since n is the only nonfundamental number in Eq. (31.8).] We turn now to calculating what field Ea the charges in the material will produce. (To help you keep track of the many symbols we have used up to now, and will be using in the rest of our calculation, we have put them all together in Table 31–1.)
Table 31–1
Symbols used in the calculations
Es= field from the source
Ea= field produced by charges in the plate
Δz= thickness of the plate
z= perpendicular distance from the plate
n= index of refraction
ω= frequency (angular) of the radiation
N= number of charges per unit volume in the plate
η= number of charges per unit area of the plate
qe= charge on an electron
m= mass of an electron
ω0= resonant frequency of an electron bound in an atom
If the source S (of Fig. 31–1) is far off to the left, then the field Es will have the same phase everywhere on the plate, so we can write that in the neighborhood of the plate
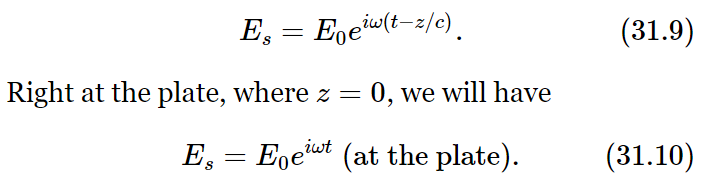
Each of the electrons in the atoms of the plate will feel this electric field and will be driven up and down (we assume the direction of E0 is vertical) by the electric force qE. To find what motion we expect for the electrons, we will assume that the atoms are little oscillators, that is, that the electrons are fastened elastically to the atoms, which means that if a force is applied to an electron its displacement from its normal position will be proportional to the force.
You may think that this is a funny model of an atom if you have heard about electrons whirling around in orbits. But that is just an oversimplified picture. The correct picture of an atom, which is given by the theory of wave mechanics, says that, so far as problems involving light are concerned, the electrons behave as though they were held by springs. So we shall suppose that the electrons have a linear restoring force which, together with their mass m, makes them behave like little oscillators, with a resonant frequency ω0. We have already studied such oscillators, and we know that the equation of their motion is written this way:
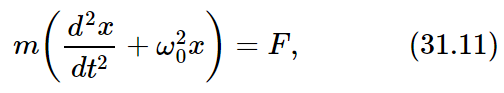
where F is the driving force.
For our problem, the driving force comes from the electric field of the wave from the source, so we should use
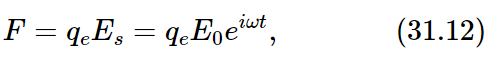
where qe is the electric charge on the electron and for Es we use the expression Es=E0eiωt from (31.10). Our equation of motion for the electron is then
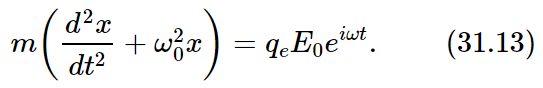
We have solved this equation before, and we know that the solution is

where, by substituting in (31.13), we find that

We have what we needed to know—the motion of the electrons in the plate. And it is the same for every electron, except that the mean position (the “zero” of the motion) is, of course, different for each electron.
Now we are ready to find the field Ea that these atoms produce at the point P. what field is produced by a sheet of charges that all move together. Referring back to Eq. (30.19), we see that the field Ea at P is just a negative constant times the velocity of the charges retarded in time by the amount z/c. Differentiating x in Eq. (31.16) to get the velocity, and sticking in the retardation [or just putting x0 from (31.15) into (30.18)] yields
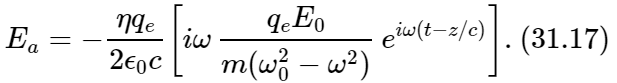
Just as we expected, the driven motion of the electrons produced an extra wave which travels to the right (that is what the factor eiω(t−z/c) says), and the amplitude of this wave is proportional to the number of atoms per unit area in the plate (the factor η) and also proportional to the strength of the source field (the factor E0). Then there are some factors which depend on the atomic properties (qe, m, and ω0), as we should expect.
The most important thing, however, is that this formula (31.17) for Ea looks very much like the expression for Ea that we got in Eq. (31.8) by saying that the original wave was delayed in passing through a material with an index of refraction n. The two expressions will, in fact, be identical if
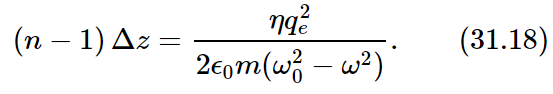
Notice that both sides are proportional to Δz, since η, which is the number of atoms per unit area, is equal to N Δz, where N is the number of atoms per unit volume of the plate. Substituting N Δz for η and cancelling the Δz, we get our main result, a formula for the index of refraction in terms of the properties of the atoms of the material—and of the frequency of the light:
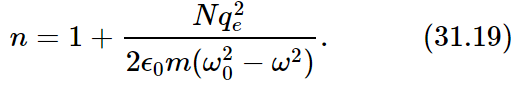
This equation gives the “explanation” of the index of refraction that we wished to obtain.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|