


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-09-03
التاريخ: 2024-02-29
التاريخ: 28-12-2016
التاريخ: 2024-09-26
|
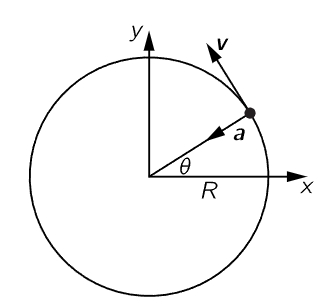
Fig. 21–2. A particle moving in a circular path at constant speed.
The fact that cosines are involved in the solution of Eq. (21.2) suggests that there might be some relationship to circles. This is artificial, of course, because there is no circle actually involved in the linear motion—it just goes up and down. We may point out that we have, in fact, already solved that differential equation when we were studying the mechanics of circular motion. If a particle moves in a circle with a constant speed v, the radius vector from the center of the circle to the particle turns through an angle whose size is proportional to the time. If we call this angle θ=vt/R (Fig. 21–2) then dθ/dt= ω0= v/R. We know that there is an acceleration a= v2/R= ω20R toward the center. Now we also know that the position x, at a given moment, is the radius of the circle times cos θ, and that y is the radius times sin θ:
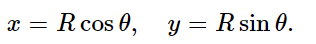
Now what about the acceleration? What is the x-component of acceleration, d2x/dt2? We have already worked that out geometrically; it is the magnitude of the acceleration times the cosine of the projection angle, with a minus sign because it is toward the center.
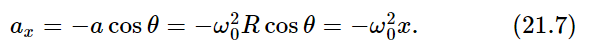
In other words, when a particle is moving in a circle, the horizontal component of its motion has an acceleration which is proportional to the horizontal displacement from the center. Of course, we also have the solution for motion in a circle: x=R cos ω0t. Equation (21.7) does not depend upon the radius of the circle, so for a circle of any radius, one finds the same equation for a given ω0. Thus, for several reasons, we expect that the displacement of a mass on a spring will turn out to be proportional to cos ω0t, and will, in fact, be exactly the same motion as we would see if we looked at the x-component of the position of an object rotating in a circle with angular velocity ω0. As a check on this, one can devise an experiment to show that the up-and-down motion of a mass on a spring is the same as that of a point going around in a circle. In Fig. 21–3 an arc light projected on a screen casts shadows of a crank pin on a shaft and of a vertically oscillating mass, side by side. If we let go of the mass at the right time from the right place, and if the shaft speed is carefully adjusted so that the frequencies match, each should follow the other exactly. One can also check the numerical solution we obtained earlier with the cosine function, and see whether that agrees very well.
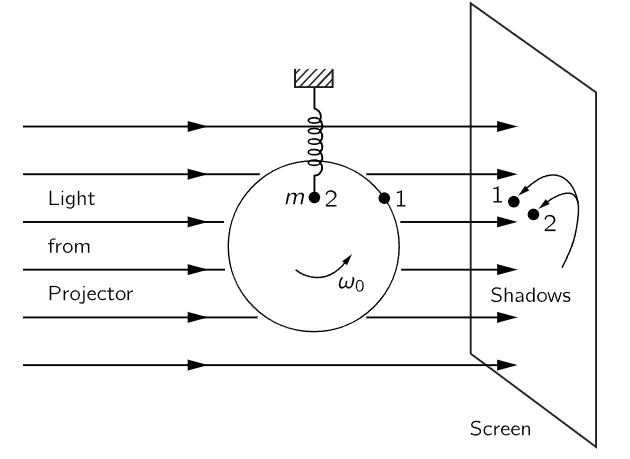
Fig. 21–3. Demonstration of the equivalence between simple harmonic motion and uniform circular motion.
Here we may point out that because uniform motion in a circle is so closely related mathematically to oscillatory up-and-down motion, we can analyze oscillatory motion in a simpler way if we imagine it to be a projection of something going in a circle. In other words, although the distance y means nothing in the oscillator problem, we may still artificially supplement Eq. (21.2) with another equation using y, and put the two together. If we do this, we will be able to analyze our one-dimensional oscillator with circular motions, which is a lot easier than having to solve a differential equation. The trick in doing this is to use complex numbers.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|