


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-01-04
التاريخ: 22-11-2020
التاريخ: 27-1-2016
التاريخ: 8-9-2017
|
The next problem to be discussed is much more difficult than the above; it has to do with the case when the forces are not constant, or simply vertical, as they were in the cases we have worked out. We want to consider a planet, for example, moving around the sun, or a satellite in the space around the earth.
We shall first consider the motion of an object which starts at some point 1 and falls, say, directly toward the sun or toward the earth (Fig. 13–2). Will there be a law of conservation of energy in these circumstances? The only difference is that in this case, the force is changing as we go along, it is not just a constant. As we know, the force is −GM/r2 times the mass m, where m is the mass that moves. Now certainly when a body falls toward the earth, the kinetic energy increases as the distance fallen increases, just as it does when we do not worry about the variation of force with height. The question is whether it is possible to find another formula for potential energy different from mgh, a different function of distance away from the earth, so that conservation of energy will still be true.

Fig. 13–2. A small mass m falls under the influence of gravity toward a large mass M.
This one-dimensional case is easy to treat because we know that the change in the kinetic energy is equal to the integral, from one end of the motion to the other, of −GMm/r2 times the displacement dr:
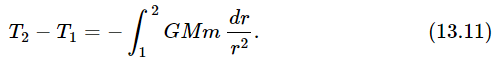
There are no cosines needed for this case because the force and the displacement are in the same direction. It is easy to integrate dr/r2; the result is −1/r, so Eq. (13.11) becomes
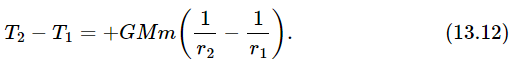
Thus, we have a different formula for potential energy. Equation (13.12) tells us that the quantity (1/2 mv2−GMm/r) calculated at point 1, at point 2, or at any other place, has a constant value.
We now have the formula for the potential energy in a gravitational field for vertical motion. Now we have an interesting problem. Can we make perpetual motion in a gravitational field? The gravitational field varies; in different places it is in different directions and has different strengths. Could we do something like this, using a fixed, frictionless track: start at some point and lift an object out to some other point, then move it around an arc to a third point, then lower it a certain distance, then move it in at a certain slope and pull it out some other way, so that when we bring it back to the starting point, a certain amount of work has been done by the gravitational force, and the kinetic energy of the object is increased? Can we design the curve so that it comes back moving a little bit faster than it did before, so that it goes around and around and around, and gives us perpetual motion? Since perpetual motion is impossible, we ought to find out that this is also impossible. We ought to discover the following proposition: since there is no friction the object should come back with neither higher nor lower velocity—it should be able to keep going around and around any closed path. Stated in another way, the total work done in going around a complete cycle should be zero for gravity forces, because if it is not zero, we can get energy out by going around. (If the work turns out to be less than zero, so that we get less speed when we go around one way, then we merely go around the other way, because the forces, of course, depend only upon the position, not upon the direction; if one way is plus, the other way would be minus, so unless it is zero we will get perpetual motion by going around either way.)
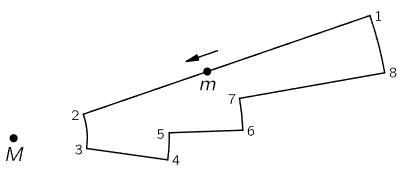
Fig. 13–3. A closed path in a gravitational field.
Is the work really zero? Let us try to demonstrate that it is. First, we shall explain more or less why it is zero, and then we shall examine it a little better mathematically. Suppose that we use a simple path such as that shown in Fig. 13–3, in which a small mass is carried from point 1 to point 2, and then is made to go around a circle to 3, back to 4, then to 5, 6, 7, and 8, and finally back to 1. All of the lines are either purely radial or circular, with M as the center. How much work is done in carrying m around this path? Between points 1 and 2, it is GMm times the difference of 1/r between these two points:
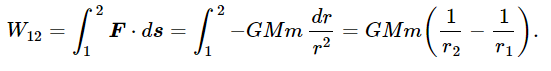
From 2 to 3 the force is exactly at right angles to the curve, so that W23≡0. The work from 3 to 4 is
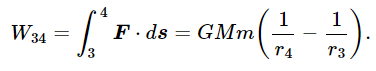
In the same fashion, we find that W45=0, W56 = GMm (1/r6−1/r5), W67=0, W78= GMm (1/r8−1/r7), and W81=0. Thus
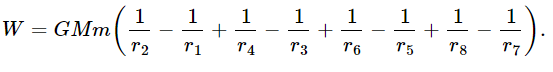
But we note that r2=r3, r4=r5, r6=r7, and r8=r1. Therefore W=0.
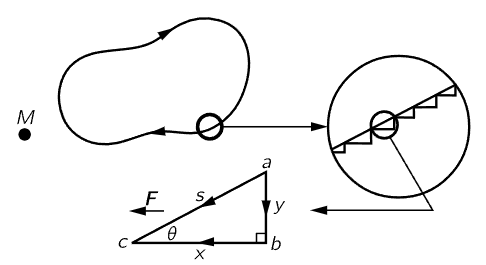
Fig. 13–4. A “smooth” closed path, showing a magnified segment of it approximated by a series of radial and circumferential steps, and an enlarged view of one step.
Of course, we may wonder whether this is too trivial a curve. What if we use a real curve? Let us try it on a real curve. First of all, we might like to assert that a real curve could always be imitated sufficiently well by a series of sawtooth jiggles like those of Fig. 13–4, and that therefore, etc., Q.E.D., but without a little analysis, it is not obvious at first that the work done going around even a small triangle is zero. Let us magnify one of the triangles, as shown in Fig. 13–4. Is the work done in going from a to b and b to c on a triangle the same as the work done in going directly from a to c? Suppose that the force is acting in a certain direction; let us take the triangle such that the side bc is in this direction, just as an example. We also suppose that the triangle is so small that the force is essentially constant over the entire triangle. What is the work done in going from a to c? It is
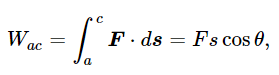
since the force is constant. Now let us calculate the work done in going around the other two sides of the triangle. On the vertical side ab the force is perpendicular to ds, so that here the work is zero. On the horizontal side bc,
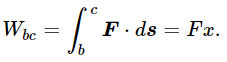
Thus we see that the work done in going along the sides of a small triangle is the same as that done going on a slant, because s cos θ is equal to x. We have proved previously that the answer is zero for any path composed of a series of notches like those of Fig. 13–3, and also that we do the same work if we cut across the corners instead of going along the notches (so long as the notches are fine enough, and we can always make them very fine); therefore, the work done in going around any path in a gravitational field is zero.
This is a very remarkable result. It tells us something we did not previously know about planetary motion. It tells us that when a planet moves around the sun (without any other objects around, no other forces) it moves in such a manner that the square of the speed at any point minus some constants divided by the radius at that point is always the same at every point on the orbit. For example, the closer the planet is to the sun, the faster it is going, but by how much? By the following amount: if instead of letting the planet go around the sun, we were to change the direction (but not the magnitude) of its velocity and make it move radially, and then we let it fall from some special radius to the radius of interest, the new speed would be the same as the speed it had in the actual orbit, because this is just another example of a complicated path. So long as we come back to the same distance, the kinetic energy will be the same. So, whether the motion is the real, undisturbed one, or is changed in direction by channels, by frictionless constraints, the kinetic energy with which the planet arrives at a point will be the same.
Thus, when we make a numerical analysis of the motion of the planet in its orbit, as we did earlier, we can check whether or not we are making appreciable errors by calculating this constant quantity, the energy, at every step, and it should not change. For the orbit of Table 9–2 the energy does change,1 it changes by some 1.5 percent from the beginning to the end. Why? Either because for the numerical method we use finite intervals, or else because we made a slight mistake somewhere in arithmetic.
Let us consider the energy in another case: the problem of a mass on a spring. When we displace the mass from its balanced position, the restoring force is proportional to the displacement. In those circumstances, can we work out a law for conservation of energy? Yes, because the work done by such a force is
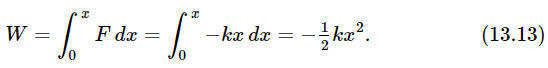
Therefore, for a mass on a spring we have that the kinetic energy of the oscillating mass plus 1/2 kx2 is a constant. Let us see how this works. We pull the mass down; it is standing still and so its speed is zero. But x is not zero, x is at its maximum, so there is some energy, the potential energy, of course. Now we release the mass and things begin to happen (the details not to be discussed), but at any instant the kinetic plus potential energy must be a constant. For example, after the mass is on its way past the original equilibrium point, the position x equals zero, but that is when it has its biggest v2, and as it gets more x2 it gets less v2, and so on. So, the balance of x2 and v2 is maintained as the mass goes up and down. Thus, we have another rule now, that the potential energy for a spring is 1/2 kx2, if the force is −kx.
________________________________________
margin
1- The energy per unit mass is 12(v2x+v2y) −1/r in the units of Table 9–2.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|