علاقات مهمة:

1- احسب قيمة F لوحدة بنائية تحتوي على ذرة واحدة عند المركز أي أن إحداثياتها 0، 0، 0.

الحل:

أي أن F² لا تعتمد على hkl ولها نفس القيمة لجميع الانعكاسات.

2- احسب قيمة F لوحدة بنائية متمركزة في القاعدة حيث تحتوي على ذرتين من نفس النوع في كل وحدة عند الأماكن 0 0 0 ، 0 1/2 1/2

الحل:

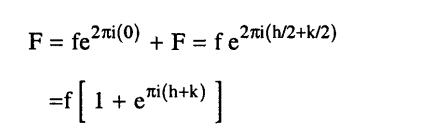
وحيث (h + k) إن دائما أعداد صحيحة فبالتالي تكون F كمية حقيقية وليست كمية مركبة وإذا كانت قيم h، k إما كليهما كميات زوجية أو كليهما كميات فردية فإن مجموعهما يكون دائما زوجيا وله القيمة 1 + للمقدار

e^πi(h+k)

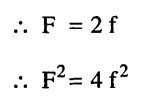
أما إذا كانت قيمh ، k أحدهما فردي والآخر زوجي، فإن مجموعهما يكون فرديا وتكون قيمة

e^πi(h+k)

مساوية -1.

ويجب ملاحظة أنه في كلتا الحالتين يكون المعامل l ليس له تأثير على معامل التركيب، وعلى سبيل المثال نكون الانعكاسات 111، 112، 113، 021، 022، 023 كلها لها نفس قيمة F وهي f2 وبالمثل تكون الانعكاسات 103، 102، 101 013، 012، 011 كلها لها قيمة للمعامل التركيبي مساوية للصفر.

3- احسب المعامل التركيبي لوحدة متمركزة في الوسط أي أن بها ذرة في الوضع وأخرى عند 1/2، 1/2، 1/2

4- احسب المعامل التركيبي لشبيكة متمركزة في الأوجه تتبع النظام المكعبي أي أن الوحدة البنائية تحتوي على أربع ذرات من نفس النوع متمركزة في المواقع 0، 0، 0؛ 0، 1/2، 1/2؛ 1/2، 0، 1/2؛ 1/2، 1/2، 0

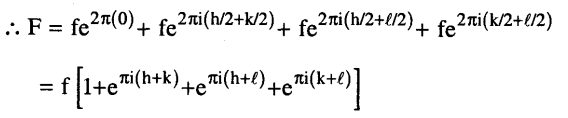
وإذا كانت قيم h، k، l إما كلها زوجية أو كلها فردية فإن القيم (h+k)، (h+l) (k+l) تكون قيما صحيحة زوجية وكل مقدار في المعادلة السابقة له قيمة تساوي الواحد الصحيح.

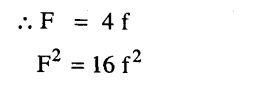
أما إذا كانت قيم h، k، l تأخذ أي قيم سواء زوجية أو فردية عندئذ يكون مجموع المقادير الأسية الثلاثة تساوي 1- سواء أكان اثنان من المعاملات فردية والمعامل الثالث زوجيا أو كان اثنان منهم زوجيا والثالث فرديا.

على سبيل المثال 012

عندئذ يكون:

F = f(1–1 +1–1) = 0

ولا يحدث انعكاس حيث 0 = F²

وعلى هذا فإن الانعكاس سوف يحدث للمستويات (111)، (200)، (220) وليس للانعكاسات (100)، (210)، (112).