James Clerk Maxwell

Vector Lessons

Maxwell's electromagnetic theory is a story of electric and magnetic fields of forces. These forces, like all others, not only have a certain magnitude but also a direction. In addition to force, velocity, momentum, and acceleration are also directional. Non-directional quantities, called “scalars,” are equally important in physics; energy, temperature, and volume are examples. All directional physical quantities are represented mathematically as “vectors,” and are distinguished from scalar quantities by their boldface symbols. A force vector might be represented by F, a velocity vector by v, and a momentum vector by p.

       Directions of vectors are conveniently specified by resolving their components in three mutually perpendicular directions, which one can picture as east-west, north south, and up down axes. The abstract symbols x , y, and z conventionally label these axes, and the vector components measured along the axes are given corresponding labels. The velocity vector v, for example, has components designated v_x, v_y, and v_z along the x , y, and z axes. An airplane climbing with a speed of 500 miles per hour at an angle of 30^o and in a southeast direction has the velocity components v_x = v_y = 306 miles per hour (southeast) and v_z = 250 miles per hour (up). See figure 1.1 for a visualization of this vector. Entire equations can be expressed in this vectorial language. Newton's second law of motion, for example, connects the force vector F with the rate of change in the momentum vector p,

Maxwell eventually put all of his electromagnetic field equations in vectorial format, and they are still seen that way. The electric and magnetic fields are represented by the vectors E and B, and Maxwell’s equations relate these vectors to the electric charges and currents always associated with an electromagnetic

Figure 1.1. Picture of a velocity vector v (represented by the arrow) for an airplane headed southeast at 500 miles per hour and climbing at an angle of 30^o.

field. Maxwell relied on two key mathematical operations for analyzing a field to reveal its charge and current structure. Both lead to differential equations and were borrowed from the dynamics of fluid motion. One operation, applied at a point in the field, measured what Maxwell called the “convergence,” that is, the extent to which the field was aimed at the point. The second operation measured the rotational character of the field at the point. For this, Maxwell eventually settled on the term “curl,” after discarding “rotation,” “whirl,” “twist,” and “twirl.” See figure 1.2 for Maxwell's illustrations of the convergence and curl operations. In later usage, it was found more convenient to switch the sign and direction of Maxwell's convergence operation and make it into “divergence.”

Great Guns

Maxwell's first paper on electromagnetism, published while he was at Aberdeen and twenty four years old, had the title On Faraday’s Lines of Force. It was aimed at giving mathematical form to Faraday's field concept. Maxwell was following Thomson, who had earlier composed a mathematical theory of Faraday's concept of electric lines of force. When he started his work, Maxwell wrote to Thomson warning him to expect some “poaching”: “I do not know the Game-laws & Patent laws of science. Perhaps the [British] Association may do something to fix them but I certainly intend to poach among your images, and as for the hints you have dropped about the ‘higher’ electricity, I intend to take them.” Thomson cheerfully opened the gates to his “electrical preserves,” wishing Maxwell good hunting.

    And Maxwell found it. His theory delved deeper than Thomson's; it concerned

Figure 1.2. Maxwell’s representations of convergence and curl operations at a point in a field.

magnetic fields as well as electric fields, and showed mathematically how they were interconnected. He found his mathematical ideas in an analogy between Faraday's lines of force and the lines of flow in a fictitious, weightless, incompressible fluid. Like all of the analogies evoked by Maxwell, this one did not constitute a complete physical theory. The gift of the analogy was a short list of equations that accounted for many of the observed phenomena of electricity, magnetism, and electromagnetism. The ingredients of the equations were five vectors, which we now write A, B, E, H, and J. (The vector notation was not fully developed until later by Oliver Heaviside and Willard Gibbs, but the anachronism violates only the letter, not the spirit, of Maxwell's equations.) The electric field was represented by the E vector, and J described electric current. For the magnetic field two vectors were required, B and H. H was generated by the currents J, as observed in Oersted’s experiment. The second magnetic vector, B, was equal to H in a vacuum but differed from it in a material medium.

       The four vectors B, E, H, and J and their equations unified in concise mathematical form the phenomena observed by Faraday, Ampere, and Oersted. The fifth vector, A, was pure Maxwellian speculation. It stood for what Faraday had originally called the “electrotonic state,” the special condition created in a wire by a magnet, such that when the wire was moved an electric current was induced. Faraday had changed his mind, however, and eventually abandoned the idea of the electrotonic condition. Maxwell resurrected the concept by introducing his vector A, which he called the “electrotonic intensity,” and showing in one of his equations that the electric field vector E was equal to the rate of change of A; that equation was a direct statement of Faraday's law of magnetic induction.

        The further history of Maxwell's seemingly innocent vector A is interesting. Maxwell changed its name twice, from the original “electrotonic intensity” to “electromagnetic momentum,” and then to “vector potential.” Maxwell's immediate successors found A offensive and wrote it out of the equations. The next generation brought it back, and in 1959 David Bohm and Yakir Aharanov gave the elusive A a secure place in electromagnetic theory by showing that without it the field is not fully specified.

      After reading an offprint of Maxwell's paper sent courtesy of the author, Faraday responded in a letter that deserves a place in any collection of great scientific correspondence. Faraday expressed his gratitude, apologized for his mathematical innocence, and then made an astonishing suggestion:

MY DEAR SIR—I received your paper, and thank you for it. I do not venture to thank you for what you have said about “Lines of Force,” because I know you have done it for the interests of philosophical truth, but you must suppose it is a work grateful to me, and gives me much encouragement to think on. I was at first almost frightened when I saw such mathematical force made to bear on the subject, and then wondered to see the subject stood it so well. I send by this post another paper to you; I wonder what you will say of it. I hope however, that bold as the thoughts may be, you may perhaps find reason to bear with them. I hope this summer to make some experiments on the time [speed] of magnetic action, or rather on the time required for the assumption of the state round a wire carrying a current, that may help the subject on. The time must probably be short as the time of light; but the greatness of the result, if affirmative, makes me not despair. Perhaps I had better have said nothing about it, for I am often long in realizing my intentions, and a failing memory is against me. Ever yours most truly, M. Faraday.

This was Faraday, nearing the end of his career, communicating with Maxwell, age twenty-six and in his second year at Aberdeen. Maxwell's paper was lengthy and full of equations, and Faraday understood little of the mathematical language. Yet he divined Maxwell's message, and was reminded of his own conjecture, that magnetic (and presumably electric) effects were transmitted in a finite time, not instantaneously. That time was indeed very short, and Faraday's experiments were not successful. But for Maxwell, the theorist, here was a grand revelation. “The idea of the time of magnetic action . . . seems to have struck Maxwell like a bolt out of the blue,” writes Martin Goldman, a Maxwell biographer. “If electromagnetic effects were not instantaneous that would of course be marvelous ammunition for lines of force, for what could a force be in transit, having left its source but not yet arrived at its target, if not some sort of traveling fluctuation along the lines of force?”

        Maxwell's next paper on electromagnetism matched Faraday's conjecture with another. This paper came from London in 1861 and 1862 with the title On Physical Lines of Force. It worked the Maxwellian wizardry with a new analogy, this one between the medium through which electric and magnetic forces were transmitted called the “ether” by Victorian scientists and the complicated honeycomb-like system of vortex motion shown in figure 1.3. Each cell in the honeycomb represented a vortex, with its axis parallel to the magnetic lines of force. The circles between the cells depicted small particles of electricity that rolled between the vortices like ball bearings and carried electric currents. Maxwell cautioned that this mechanical ether model, like the analogy he used in his previous paper, was to be used with care: “I do not bring it forward as a mode of connection existing in nature, or even as that which I would willingly assent to as an electrical hypothesis. It is, however, a mode of connection which is mechanically conceivable, and easily investigated, and it serves to bring out the actual mechanical connections between the known electromagnetic phenomena; so that I venture to say that anyone who understands the provisional and temporary character of this hypothesis, will find himself helped rather than hindered by it in his search after the true interpretation of the phenomena.”

      Maxwell endowed his vortices and the real ether with a physical property that was crucial in the further evolution of his theory: they were elastic. He knew

Figure 1.3. Maxwell’s vortex model of the ether.

that elastic media of all kinds support transverse wave motion (“transverse” here means perpendicular to the direction of wave propagation), and that the speed of the wave depends on a certain elasticity parameter of the medium. It happened that Maxwell could calculate a value for that parameter from his ether model, and from that the speed of the electromagnetic waves he imagined were propagated through the elastic medium. He did the calculation, and found to hi amazement that the result was almost identical to the speed of light that had been measured in Germany by Wilhelm Weber and Rudolph Kohlrausch. In uncharacteristic italics, Maxwell announced his conclusion: “We can scarcely avoid the conclusion that light consists of the transverse undulations of the same medium which is the cause of electric and magnetic phenomena.”

          Light as traveling electromagnetic waves: it was a simple idea, yet its implications for science and technology were still being realized a hundred years later. Maxwell had brought together under the great umbrella of his equations two great sciences, electromagnetism and optics, previously thought to be unrelated; now Maxwell claimed they were close relatives.

        Like most revolutionary developments in science, Maxwell's concept of electromagnetic waves was slow to catch on. Eventually, two decades after Maxwell's Physical Lines of Force paper, experimentalists began to think about how to generate, detect, and use electromagnetic waves. At first, they tried to make “electromagnetic light,” and that effort failed. Then they looked for electromagnetic waves of a greatly different kind and succeeded spectacularly. The hero in that work was Heinrich Hertz, the Mozart of physics, a man who had immense talent and a short life. We will come to his story later.

       Hertz's waves were what we now call radio waves and microwaves. In a primitive form, radio communication, and its offspring, television, were born in Hertz's laboratory. As we now recognize, radio waves, microwaves, and light waves are “colors” in a vast continuous electromagnetic rainbow. Distinguished by their wavelengths, radio waves and microwaves are long, and light waves short. Between are the electromagnetic “colors” we call infrared radiation. On the short-wavelength side of visible light are ultraviolet radiation, x rays, and gamma rays. Wavelengths of radio waves and gamma rays differ by an astronomical ten orders of magnitude. These discoveries came to light during the last decade of the nineteenth century and the first two of the twentieth, sadly too late for Maxwell and Hertz to witness.

        Maxwell extracted another, more subtle, conclusion from the elasticity property of his ether model. When the vortices were stretched or compressed in a changing electric field, the particles of electricity between the vortices were displaced, and their movement constituted what Maxwell called a “displacement current.” Like any other current, it could generate a magnetic field a la Oersted, and Maxwell incorporated this possibility into his equations. With that addition, Maxwell's list of equations, although different in form, told the same mathematical story as the “Maxwell equations” found in modern textbooks.

         In early 1865, Maxwell wrote to his cousin Charles Cay (later in the same year the recipient of Maxwell's “heart, head, and fingers” advice): “I have also a paper afloat, with an electromagnetic theory of light, which till I am convinced to the contrary, I hold to be great guns.” This was his third offering on electromagnetism, A Dynamical Theory of the Electromagnetic Field, considered by most commentators to be his crowning achievement. He explained the title this way: “The theory I propose may . . . be called a theory of the Electromagnetic Field, because it has to do with the space in the neighborhood of the electric or magnetic bodies, and it may be called a Dynamical theory, because it assumes that in that space there is matter in motion, by which the observed electromagnetic phenomena are produced.”

      The “matter in motion” was, as before in his Lines of Force papers, the ether, but he now treated it without the mechanistic trappings. Gone were the fluids, vortices, and particles of electricity. In their place was an abstract analytical method introduced in the eighteenth century by Joseph Lagrange as a generalization of Newton's system of mechanics. The great advantage of Lagrange's approach was that it did its work above and beyond the world of hidden mechanisms. The mechanisms might actually be there (for example, in the ether), but the Lagrangian theorist had no obligation to worry about them.

        Thomson and P. G. Tait, in their comprehensive Treatise on Natural Philosophy, had made abundant use of Lagrange's analytical mechanics, and in a review of the Treatise Maxwell explained that Lagrange's method was a “mathematical illustration of the scientific principle that in the study of any complex object, we must fix our attention on those elements of it which we are able to observe and to cause to vary, and ignore those which we can neither observe nor cause to vary.” And for the mystified he offered a metaphor: “In an ordinary belfry, each bell has one rope which comes down through a hole in the floor to the bellringer's room. But suppose that each rope, instead of acting on one bell, contributes to the motion of many pieces of machinery, and that the motion of each piece is determined not by the motion of one rope alone, but that of several, and suppose, further, that all this machinery is silent and utterly unknown to the men at the ropes, who can only see as far as the holes in the floor.” Each of the bellringer's ropes supplies its own information, and the ropes can be manipulated to obtain the potential energy and kinetic energy of the complex system of bells. Applying Lagrange's methods, “these data are sufficient to determine the motion of every one of the ropes when it and all the others are acted on by any given forces. This is all that the men at the ropes can ever know. If the machinery above has more degrees of freedom than there are in the ropes, the coordinates which express these degrees of freedom must be ignored. There is no help for it.”

      Where it provides escape from some otherwise weird predictions of quantum theory. Quantum theorists do not practice Lagrangian mechanics, but for different reasons they see themselves as Maxwellian bellringer's. If there is a hidden world beneath their essentially statistical description, they are obliged to omit it from their deliberations, and “there is no help for it.”

        Maxwell used the Lagrangian method to derive all of the mathematical equipment he had obtained earlier in his Lines of Force papers, and then went further to identify his vector A as a measure of “electromagnetic momentum,” and to calculate the energy of the electromagnetic field. With these additional elements, his theory of electromagnetism was complete. About a decade later, in 1873, Maxwell summarized his theory, and many other aspects of electromagnetism, in a difficult two-volume work called A Treatise on Electromagnetism, which has been called (not entirely as a compliment) the Principia of electromagnetism. In the Treatise, Maxwell's equations are found almost in the modern vectorial format.

     Maxwell pursued numerous topics besides electromagnetism in his researches, including gas theory, thermodynamics, Saturn's rings, and color vision. His molecular theory of gases, another “dynamical” theory, ranks a close second in importance to his theory of the electromagnetic field. It brought another revolutionary development to physics, the first use of statistical methods to describe macroscopic systems of molecules. In the hands of first Boltzmann and then Gibbs, Maxwell's statistical approach became the fine theoretical tool now called “statistical mechanics.”

Heinrich Hertz

When Maxwell died in 1879, his theory of the electromagnetic field and it's amazing progeny, electromagnetic waves, had little experimental support, just the indirect evidence that Maxwell's calculated speed of the electromagnetic waves matched the speed of light.

        Maxwell's immediate successors thought about electromagnetic waves, but at first could find no feasible way to study them in the laboratory. The turning point, in both the study of electromagnetic waves and the fortunes of Maxwell’s theory, came with the force of an intellectual earthquake in a series of experiments brilliantly carried out by Heinrich Hertz.

        The year was 1887, and Hertz had recently arrived at the Karlsruhe Technische Hochschule, Baden, Germany. He was only thirty years old, but already well known, and rising rapidly in the academic world. He had been Helmholtz's star research student in Berlin, then briefly Privatdozent (instructor) at the University of Kiel, and was now a full professor at Karlsruhe.

       When he took up his work in Karlsruhe, Hertz was familiar with Maxwell's theory but not committed to it. Earlier, Helmholtz had tried to interest him in the problem of creating experiments to test Maxwell's assumptions (with a prestigious prize attached), but Hertz had tactfully declined. His aim now was to assemble an apparatus for studying electrical discharges in gases. One item of equipment in the Karlsruhe laboratory was a spark generator called a Ruhmkorff coil (distantly related to the ignition coil that generates sparks in a gasoline engine). He tinkered with the coil and was intrigued by its performance in the configuration depicted in figure 1.4. The coil A was connected to two small brass spheres B separated by 3⁄4 centimeter, and also to two straight lengths of thick copper wires 3 meters in length terminating in two metallic spheres, 30 centimeters in diameter. When the coil was activated, sparks were repeatedly generated in the gap at B.

          Hertz found that he could connect the coil circuit electrically to a wire loop, as shown in figure 1.5, and with careful adjustment of the size of the loop, obtain observable sparks across the gap M. He then discovered that he could obtain

sparks in the wire loop with the connecting wire removed (fig. 1.6).

             If there was no wire linking the two circuits electrically, how were they communicating with each other? At this point, Hertz began to realize that his device was generating and detecting electromagnetic waves. The origin of the waves

Figure 1.4. Hertz’s coil circuit. This figure and the two following are adapted from Heinrich Hertz, “On Very Fast Electric Oscillations,” in Wiedemann’s Annalen der Physik und Chemie 31 (1887).

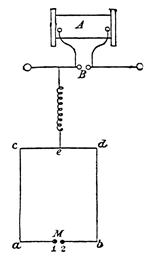
Figure 1.5. Hertz’s coil circuit connected to a wire loop with a spark gap.

was a sequence of electrical oscillations initiated by each spark in the coil circuit. The waves were propagated along a wire or even through free space to the wire loop, and their presence revealed by the observed sparks at the gap in the loop.

           Waves of all kinds have three fundamental characteristics: a wavelength, the distance from one wave crest to the next; a frequency, a count of the number of wave cycles passing a certain point in a unit of time; and a speed of propagation, the distance traveled by a wave crest in a unit of time. Hertz was, above all, interested in the speed of his waves. Was that speed finite? If so, Maxwell's theory was strongly supported against its competitors, based on the concept of action at a distance and an infinite speed of propagation. Hertz soon found a route to that crucial determination. He relied on a simple equation, valid for all kinds of waves, that connects the speed s, frequency v, and wavelength λ,

s = λv.          (1)

         The frequency v in this equation could be calculated from the length of the wire and the diameters of the metallic spheres in the coil circuit, using a formula derived earlier by Thomson. Hertz found the calculated frequencies to be exceptionally high, around one hundred million cycles per second. To measure the wavelength λ, Hertz ingeniously reconfigured his apparatus so it generated “standing waves” (as in a violin string), either along a straight wire or in free space, and using one of the wire-loop detectors, he located crests and troughs of the waves; the distance from one measured crest to the next was the wavelength.

Figure 1.6. Hertz’s coil circuit and wire loop disconnected. Sparks are still produced at the gap in the loop.

There were stubborn problems: he made an embarrassing calculational mistake, and the waves were distorted by an iron stove and other objects in the laboratory. But eventually equation (1) told the story Hertz was expecting: his electromagnetic waves had a finite speed, in fact, the speed of light, known to be three hundred million meters per second.

         Although he had already made a strong case for Maxwell's theory, Hertz went much further, displaying a thoroughness and ingenuity that would have impressed Faraday. He demonstrated that his electromagnetic waves could be reflected, focused, refracted, diffracted, and polarized that they were, in every sense but frequency and wavelength, the same as light waves.

       In about one “miraculous year” of experiments, Hertz had closed the great debate between the Maxwellians and the proponents of action at a distance. Not surprisingly, Hertz's work was quickly recognized in Britain, and more slowly in Germany, where action-at-a-distance sentiment was strongest. The joke was that Germans learned about Hertz by way of the British. But by the summer of 1889, Hertz's triumph was complete; at a meeting in Heidelberg, he was celebrated by Germany's great men of science. In the same year, he was appointed Clausius's successor in Bonn.

       Tragically, Hertz was as unfortunate with his health as he was fortunate with his talent. The first sign of trouble was a series of toothaches in 1888, which led to removal of all his teeth in 1889. By 1892, he was suffering from pains in his nose and throat, and was often depressed. His doctors could give him no satisfactory diagnosis. Several operations failed to provide permanent relief. By December 1893, he knew he would not recover, and in a letter he asked his parents “not to mourn . . . rather you must be a little proud and consider that I am among the especially elect destined to live for only a short while and yet to live enough. I did not choose this fate, but since it has overtaken me, I must be content; and if the choice had been left to me, perhaps I should have chosen it myself.”

      Hertz died of blood poisoning on New Year's Day, 1894; he was thirty-six years old.

“Maxwell’s Equations”

Once a scientific theory has been created, it becomes public property. Friends and enemies of the theory (and the theorist) are licensed to argue for changes in both content and form as they see fit. If the theory has been successful, its content is likely to be more or less permanent. But the form the mathematical form of a physical theory may not be so durable. Newton's geometrical mathematical language in the Principia did not last, nor did Clausius's mathematically elaborate version of entropy theory. The physical content of Newton's laws of motion and the entropy concept are, however, still with us.

       Maxwell's theory met a similar fate. Most of the physical assertions Maxwell made in his Treatise on Electricity and Magnetism are permanent fixtures. His equations, on the other hand, have been reshaped by other hands. As we find them in the Treatise, the equations are a dozen in number. Maxwell's successors, particularly Hertz and the most gifted of the British Maxwellians, Oliver Heaviside, wanted more “purity” in the equations. They suppressed auxiliary equations, eliminated the vector potential A and a companion scalar potential Ψ, and boiled the original dozen down to just four differential equations.

      These “Maxwell's equations” have as their mathematical ingredients the electric field vector E, the magnetic field vector B, the electric current vector J, and the density of electric charge ρ. There are two divergence equations and two curl equations, one each for E and B:

 div E = ρ         (2)

        (3)

div B = 0              (4)

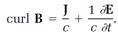 (5)

The abbreviation “div” stands for divergence, c is the speed of light, and the derivatives written with the “∂” notation are calculated just for changes in the time t, holding all other variables constant. (Mathematicians call these “partial” derivatives and the equations “partial differential equations.”) To put the equations in their most symmetrical and mathematically least excruciating form, I have assumed that the electromagnetic field is propagated in a vacuum.

         In its modern interpretation, the divergence equation (2) simply states that an electric field E is produced by electric charges (included in the density of electric charge ρ). The companion curl equation (3) for E tells us what Faraday observed: that a rotational electric field is generated in a changing magnetic field B.

       The divergence equation (4) for the magnetic field parallels equation (2) for the electric field, except that there is no magnetic counterpart of the electric charge density ρ. Here we see a fundamental difference between electricity and magnetism. One of the two kinds of electricity, positive or negative, can dominate, making the net charge density ρ positive or negative. But a magnetic field cannot be divided this way: every north pole in the field is exactly balanced by a south pole, there is no observable “magnetic charge density,” and a zero is required on the right side of the divergence equation (4).

       The second curl equation (5) asserts in its first two terms what (curl B = J/ c) Oersted observed: that a rotational magnetic field B is generated by an electric current J. The third term in equation (5), (1 ∂E /c ∂t), has special significance. Maxwell proved that without it the equation disobeys the fundamental law of electricity that electric charge, like energy, is conserved: it cannot be created or destroyed. The third term in equation (5) saves charge conservation and it represents a ubiquitous kind of electric current (Maxwell's “displacement current”), found even in free space.

        Maxwell's field theory, embodied in his equations, closed the book on the nineteenth century, or “classical,” theory of electromagnetism. It also had a long reach into the twentieth century. Einstein first found in Maxwell's equations the clue he needed drastically to revamp the concepts of space and time in his special theory of relativity, and then he followed Maxwell's electromagnetic field theory with his own gravitation field theory. More recently, quantum field theory has become the mainstay of particle physics.

      In an appreciation of Maxwell, Einstein wrote: “Before Maxwell people thought of physical reality in so far as it represented events in nature as material points, whose changes consist only in motions which are subject to total differential equations [that is, no partial derivatives]. After Maxwell they thought of physical reality as represented by continuous fields, not mechanically explicable, which are subject to partial differential equations [partial derivatives included]. This change in the conception of reality is the most profound and the most fruitful that physics has experienced since Newton.”