


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-12-2021
Date: 14-2-2017
Date: 5-1-2022
|
A relation "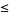 " is a partial order on a set
" is a partial order on a set 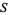 if it has:
if it has:
1. Reflexivity: 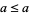 for all
for all 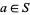 .
.
2. Antisymmetry: 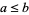 and
and 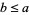 implies
implies 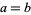 .
.
3. Transitivity: 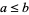 and
and 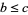 implies
implies 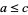 .
.
For a partial order, the size of the longest chain (antichain) is called the partial order length (partial order width). A partially ordered set is also called a poset.
A largest set of unrelated vertices in a partial order can be found using MaximumAntichain[g] in the Wolfram Language package Combinatorica` . MinimumChainPartition[g] in the Wolfram Language package Combinatorica` partitions a partial order into a minimum number of chains.
REFERENCES:
Ruskey, F. "Information on Linear Extension." http://www.theory.csc.uvic.ca/~cos/inf/pose/LinearExt.html.
Skiena, S. "Partial Orders." §5.4 in Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, pp. 203-209, 1990.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|