


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-12-2021
Date: 10-12-2021
Date: 10-12-2021
|
In order to integrate a function over a complicated domain 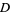 , Monte Carlo integration picks random points over some simple domain
, Monte Carlo integration picks random points over some simple domain 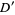 which is a superset of
which is a superset of 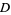 , checks whether each point is within
, checks whether each point is within 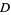 , and estimates the area of
, and estimates the area of 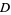 (volume,
(volume, 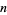 -dimensional content, etc.) as the area of
-dimensional content, etc.) as the area of  multiplied by the fraction of points falling within
multiplied by the fraction of points falling within 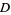 . Monte Carlo integration is implemented in the Wolfram Language as NIntegrate[f, ..., Method -> MonteCarlo].
. Monte Carlo integration is implemented in the Wolfram Language as NIntegrate[f, ..., Method -> MonteCarlo].
Picking 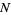 randomly distributed points
randomly distributed points 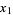 ,
, 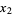 , ...,
, ..., 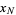 in a multidimensional volume
in a multidimensional volume 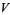 to determine the integral of a function
to determine the integral of a function 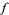 in this volume gives a result
in this volume gives a result
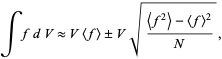 |
(1) |
where
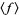 |
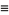 |
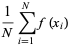 |
(2) |
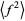 |
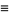 |
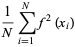 |
(3) |
(Press et al. 1992, p. 295).
REFERENCES:
Hammersley, J. M. "Monte Carlo Methods for Solving Multivariable Problems." Ann. New York Acad. Sci. 86, 844-874, 1960.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Simple Monte Carlo Integration" and "Adaptive and Recursive Monte Carlo Methods." §7.6 and 7.8 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 295-299 and 306-319, 1992.
Ueberhuber, C. W. "Monte Carlo Techniques." §12.4.4 in Numerical Computation 2: Methods, Software, and Analysis. Berlin: Springer-Verlag, pp. 124-125 and 132-138, 1997.
Weinzierl, S. "Introduction to Monte Carlo Methods." 23 Jun 2000. http://arxiv.org/abs/hep-ph/0006269.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|