المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Baker,s Map |
 947
 03:38 مساءً
date: 6-10-2021 |
Author : Lichtenberg, A. and Lieberman, M 
Book or Source : Regular and Stochastic Motion. New York: Springer-Verlag 
Page and Part : ...|
Read More
Date: 19-11-2021
1104
Date: 23-11-2021
1681
Date: 18-8-2021
1272
|
The map
 |
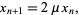(1) |
where 
is computed modulo 1. A generalized Baker's map can be defined as
 |
 |
 |
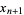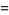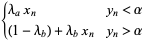(2) |
 |
 |
 |
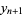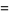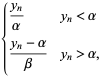(3) |
where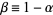 
, 
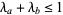, and 
and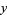 
are computed mod 1. The 
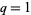q-dimension is
 |
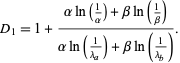(4) |
If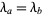 
, then the general q-dimension is
 |
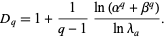(5) |
REFERENCES:
Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion. New York: Springer-Verlag, p. 60, 1983.
Ott, E. Chaos in Dynamical Systems. Cambridge, England: Cambridge University Press, pp. 81-82, 1993.
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, p. 32, 1990.
|
|
|
|
دور في الحماية من السرطان.. يجب تناول لبن الزبادي يوميا
|
|
|
|
|
|
|
العلماء الروس يطورون مسيرة لمراقبة حرائق الغابات
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|
