Exotic Sphere

Milnor (1956) found more than one smooth structure on the seven-dimensional hypersphere. Generalizations have subsequently been found in other dimensions. Using surgery theory, it is possible to relate the number of diffeomorphism classes of exotic spheres to higher homotopy groups of spheres (Kosinski 1992).

Kervaire and Milnor (1963) computed a list of the number 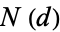 of distinct (up to diffeomorphism) differential structures on spheres indexed by the dimension  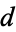of the sphere. For 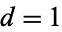, 2, ..., assuming the Poincaré conjecture, they are 1, 1, 1, 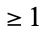, 1, 1, 28, 2, 8, 6, 992, 1, 3, 2, 16256, 2, 16, 16, ... (OEIS A001676). The status of  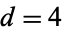is still unresolved, and it is not known whether there is 1, more than 1, or infinitely many smooth structures on the 4-sphere (Scorpan 2005). The claim that there is exactly one is known as the smooth Poincaré conjecture for .

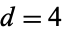The only exotic Euclidean spaces are a continuum of exotic R4 structures.

REFERENCES:

Kervaire, M. A. and Milnor, J. W. "Groups of Homotopy Spheres: I." Ann. Math. 77, 504-537, 1963.

Kosinski, A. A. §X.6 in Differential Manifolds. Boston, MA: Academic Press, 1992.

Levine, J. P. "Lectures on Groups of Homotopy Spheres." In Algebraic and Geometric Topology (New Brunswick, NJ, 1983). Berlin: Springer-Verlag, pp. 62-95, 1985.

Milnor, J. "On Manifolds Homeomorphic to the 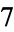-Sphere." Ann. Math. 64, 399-405, 1956.

Milnor, J. "Topological Manifolds and Smooth Manifolds." In Proc. Internat. Congr. Mathematicians (Stockholm, 1962). Djursholm: Inst. Mittag-Leffler, pp. 132-138, 1963.

Milnor, J. W. and Stasheff, J. D. Characteristic Classes. Princeton, NJ: Princeton University Press, 1973.

Monastyrsky, M. Modern Mathematics in the Light of the Fields Medals. Wellesley, MA: A K Peters, 1997.

Novikov, S. P. (Ed.). Topology I. New York: Springer-Verlag, 1996.

Scorpan, A. The Wild World of 4-Manifolds. Providence, RI: Amer. Math. Soc., 2005.

Sloane, N. J. A. Sequence A001676/M5197 in "The On-Line Encyclopedia of Integer Sequences."

Whitney, H. "The Work of John W. Milnor." In Proc. Internat. Congress Mathematicians. Stockholm, pp. 48-50, 1962.