


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-7-2021
Date: 21-6-2021
Date: 14-8-2021
|
A topological space that contains a homeomorphic image of every topological space of a certain class.
A metric space 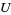 is said to be universal for a family of metric spaces
is said to be universal for a family of metric spaces 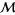 if any space from
if any space from 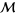 is isometrically embeddable in
is isometrically embeddable in 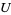 . Fréchet (1910) proved that
. Fréchet (1910) proved that 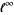 , the space of all bounded sequences of real numbers endowed with a supremum norm, is a universal space for the family
, the space of all bounded sequences of real numbers endowed with a supremum norm, is a universal space for the family 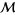 of all separable metric spaces. Holsztynski (1978) proved that there exists a metric
of all separable metric spaces. Holsztynski (1978) proved that there exists a metric 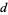 on
on 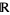 , inducing the usual topology, such that every finite metric space embeds in
, inducing the usual topology, such that every finite metric space embeds in 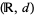 (Ovchinnikov 2000).
(Ovchinnikov 2000).
REFERENCES:
Fréchet, M. "Les dimensions d'un ensemble abstrait." Math. Ann. 68, 145-168, 1910.
Holsztynski, W. "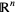 as a Universal Metric Space." Not. Amer. Math. Soc. 25, A-367, 1978.
as a Universal Metric Space." Not. Amer. Math. Soc. 25, A-367, 1978.
Ovchinnikov, S. "Universal Metric Spaces According to W. Holsztynski." 13 Apr 2000. https://arxiv.org/abs/math.GN/0004091.
Urysohn, P. S. "Sur un espace métrique universel." Bull. de Sciences Math. 5, 1-38, 1927.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|