


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-6-2017
Date: 9-6-2021
Date: 25-7-2021
|
In general, it is possible to link two 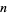 -dimensional hyperspheres in
-dimensional hyperspheres in 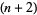 -dimensional space in an infinite number of inequivalent ways. In dimensions greater than
-dimensional space in an infinite number of inequivalent ways. In dimensions greater than 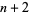 in the piecewise linear category, it is true that these spheres are themselves unknotted. However, they may still form nontrivial links. In this way, they are something like higher dimensional analogs of two one-spheres in three dimensions. The following table gives the number of nontrivial ways that two
in the piecewise linear category, it is true that these spheres are themselves unknotted. However, they may still form nontrivial links. In this way, they are something like higher dimensional analogs of two one-spheres in three dimensions. The following table gives the number of nontrivial ways that two 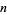 -dimensional hyperspheres can be linked in
-dimensional hyperspheres can be linked in 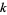 dimensions.
dimensions.
| D of spheres | D of space | distinct linkings |
| 23 | 40 | 239 |
| 31 | 48 | 959 |
| 102 | 181 | 3 |
| 102 | 182 | 10438319 |
| 102 | 183 | 3 |
Two 10-dimensional hyperspheres link up in 12, 13, 14, 15, and 16 dimensions, unlink in 17 dimensions, then link up again in 18, 19, 20, and 21 dimensions. The proof of these results consists of an "easy part" (Zeeman 1962) and "hard part" (Ravenel 1986). The hard part is related to the calculation of the (stable and unstable) homotopy groups of spheres.
REFERENCES:
Bing, R. H. The Geometric Topology of 3-Manifolds. Providence, RI: Amer. Math. Soc., 1983.
Ravenel, D. Complex Cobordism and Stable Homotopy Groups of Spheres. New York: Academic Press, 1986.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 7, 1976.
Zeeman, E. C. "Isotopies and Knots in Manifolds." In Topology of 3-Manifolds and Related Topics (Ed. M. K. Fort). Englewood Cliffs, NJ: Prentice-Hall, pp. 187-193, 1962.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|