


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-6-2021
Date: 30-5-2021
Date: 10-5-2021
|
An embedding of a 1-sphere in a 3-manifold which exists continuously over the 2-disk also extends over the disk as an embedding. An alternate phrasing is that if a knot group is isomorphic to the group of the integers 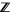 , then the knot is isomorphic to the unknot (Livingston 1993, p. 104).
, then the knot is isomorphic to the unknot (Livingston 1993, p. 104).
This theorem was proposed by Dehn in 1910, but a correct proof was not obtained until the work of Papakyriakopoulos (1957ab).
REFERENCES:
Hempel, J. 3-Manifolds. Princeton, NJ: Princeton University Press, 1976.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., 1993.
Papakyriakopoulos, C. D. "On Dehn's Lemma and the Asphericity of Knots." Proc. Nat. Acad. Sci. USA 43, 169-172, 1957a.
Papakyriakopoulos, C. D. "On Dehn's Lemma and the Asphericity of Knots." Ann. Math. 66, 1-26, 1957b.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 100-101, 1976.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|