Bland-Altman Plot

A Bland-Altman plot is a data plotting method which simultaneously presents data sets from two different tests in a way that allows for easier determination of whether the two test methods agree.

In particular, this is done by first performing two tests  and  on each of  samples. The resulting  data points are then "combined" into 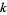 Cartesian coordinates

for , 2, ..., , where  and

In this way, the horizontal axis represents the mean of the two tests while the vertical axis represents their difference.

Bland-Altman plots are sometimes referred to as difference plots, mean-difference plots, Tukey mean-difference plots. Specific instances of Bland-Altman plots also have a tendency to show up in various areas of science and medicine under completely different names, such as the so-called MA and RA plots common in the study of DNA microarrays.

One of the motivating factors behind this technique is the observation that many experts attempt to (incorrectly) argue agreement of test methods by way of the correlation coefficient of the resulting data sets. Indeed, samples in poor agreement may in fact have high correlation (Bland and Altman 1986). Because changes in scale affect only agreement and not correlation (Fèvre 2008), transforming the data sets to plot the arithmetic mean of the two test values versus the difference thereof more accurately summarizes the connection between the results of the two tests.

REFERENCES:

Bland, J. M. and Altman, D. G. "Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement." The Lancet 327, 307-310, 1986.

Fèvre, E. "Bland-Altman Plot: Measuring Agreement Between Methods." 2008. http://imaging.mrc-cbu.cam.ac.uk/statswiki/FAQ/balt?action=AttachFile&do=get&target=balt.pdf.

Tobias, M.; Paul, S.; and Yeh, L. "Embodying Social Rank: How body Fat Varies With Social Status, Gender and Ethnicity in New Zealand." Public Health Intelligence Occasional Bulletin 34, 1-32, 2006. http://www.health.govt.nz/publication/embodying-social-rank-how-body-fat-varies-social-status-gender-and-ethnicity-new-zealand.