


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-3-2021
Date: 8-4-2021
Date: 18-3-2021
|
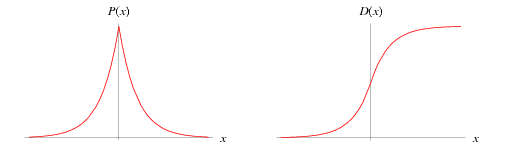
The Laplace distribution, also called the double exponential distribution, is the distribution of differences between two independent variates with identical exponential distributions (Abramowitz and Stegun 1972, p. 930). It had probability density function and cumulative distribution functions given by
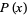 |
 |
 |
(1) |
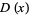 |
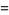 |
![1/2[1+sgn(x-mu)(1-e^(-|x-mu|/b))].](https://mathworld.wolfram.com/images/equations/LaplaceDistribution/Inline6.gif) |
(2) |
It is implemented in the Wolfram Language as LaplaceDistribution[mu, beta].
The moments about the mean 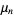 are related to the moments about 0 by
are related to the moments about 0 by
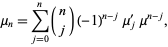 |
(3) |
where 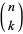 is a binomial coefficient, so
is a binomial coefficient, so
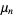 |
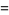 |
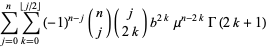 |
(4) |
 |
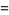 |
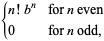 |
(5) |
where 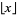 is the floor function and
is the floor function and 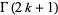 is the gamma function.
is the gamma function.
The moments can also be computed using the characteristic function,
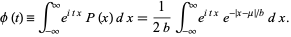 |
(6) |
Using the Fourier transform of the exponential function
=1/pi(k_0)/(k^2+k_0^2)](https://mathworld.wolfram.com/images/equations/LaplaceDistribution/NumberedEquation3.gif) |
(7) |
gives
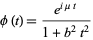 |
(8) |
(Abramowitz and Stegun 1972, p. 930). The moments are therefore
![mu_n=(-i)^nphi(0)=(-i)^n[(d^nphi)/(dt^n)]_(t=0).](https://mathworld.wolfram.com/images/equations/LaplaceDistribution/NumberedEquation5.gif) |
(9) |
The mean, variance, skewness, and kurtosis excess are
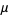 |
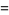 |
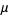 |
(10) |
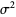 |
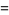 |
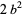 |
(11) |
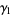 |
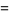 |
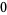 |
(12) |
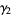 |
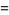 |
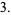 |
(13) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 104, 1984.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|