


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 21-8-2016
Date: 13-7-2016
Date: 16-3-2021
|
Deterministic and Random Correlation Dimensions
As a group, graphical relations such as Figures 1 and 2 in theory ought to show whether the data are random (mutually unrelated), on the one hand, or deterministic, on the other. Here's how. The correlation dimension or exponent v for a given embedding dimension is represented by the slope of the straight line on Figures 1 and 2. The steeper the slope, the greater the correlation dimension. The straight-line sections on those figures have a steeper slope as embedding dimension increases. Therefore, correlation dimension increases with increase in embedding dimension. If the data represent an attractor, the assigned embedding space eventually allows the attractor full self-expression. Thereafter, adding more embedding dimensions has no effect on the computed correlation dimension. For instance, a one-dimensional line is still one-dimensional whether embedded in a plane, in the atmosphere, or in any number of dimensions. Similarly, a plane is still twodimensional
whether embedded in three or more dimensions. What that means is that, as long as the embedding dimension is greater than the attractor dimension. the reconstructed attractor almost always has the same correlation dimension as the true attractor. (However, for practical considerations, we don't want an embedding dimension any larger than necessary.)
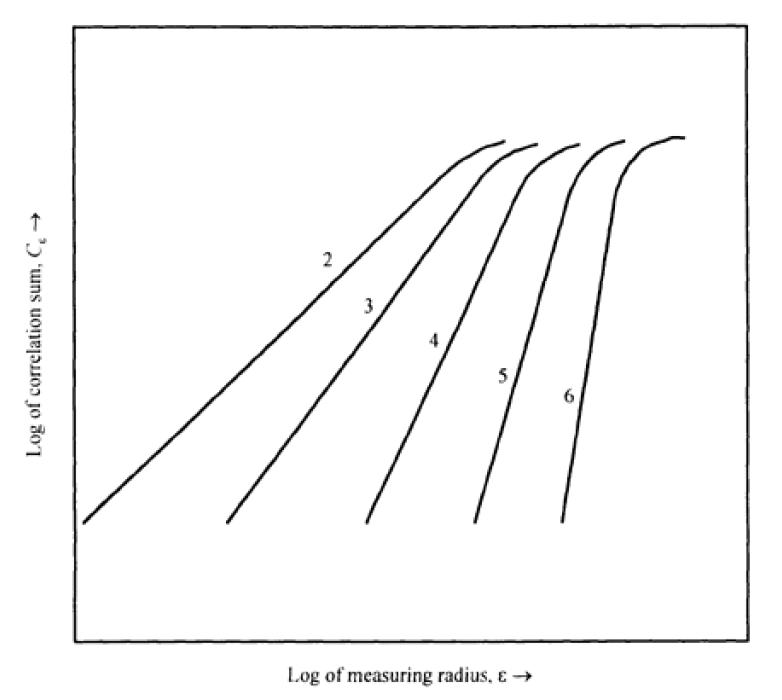
Figure 1:Idealized plot of correlation sum as a function of measuring radius. Number alongside each relation is embedding dimension.
For highly deterministic or chaotic data, therefore, the correlation dimension initially increases with increase in embedding dimension, but eventually it becomes constant. Figure 3 (lower curve) shows an idealized relation for such data. The line for chaotic data flattens and becomes approximately horizontal at (or at least asymptotic toward) some final correlation dimension. The eventual, true value of the correlation dimension has an important practical implication: the minimum number of variables needed to describe or model the system is the next highest integer value above the correlation dimension. For instance, if the correlation dimension is 2.68, three variables might be enough to model the system. Random data, in contrast, continually fill their allotted space as we increase the embedding dimension, at least for an infinite number of observations. Consequently, the slope (correlation dimension) continues to increase, without any indication of becoming asymptotic (Fig. 3).
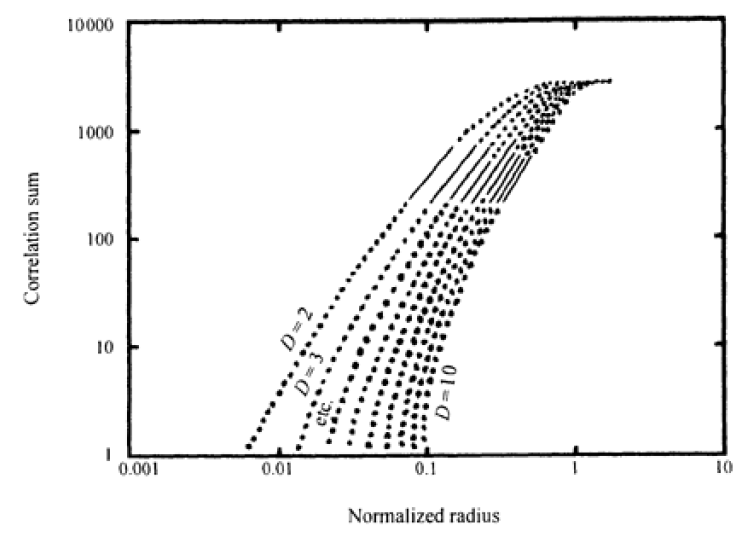
Figure 2: Correlation sum versus measuring radius for 241 years of sunspot activity (adapted from Mundt et al. 1991, with permission from the American Geophysical Union).
As I said, that's how it's supposed to work in theory. In practice, data are limited. They are also noisy. The ideal patterns described above then don't necessarily happen. For instance, random numbers treated in certain ways can show an apparent stabilization of slopes on the plot of correlation sum versus radius (e.g. Osborne & Provenzale 1989). In such case, we'd be misled into declaring a low-dimensional determinism when there wasn't any. Furthermore, a plot such as Figure 3 for real-world data often shows a tendency to reach a plateau but doesn't become flat enough to give a very precise value of that potential asymptote. For instance, shows correlation dimension versus embedding dimension for (a) laboratory populations of the sheep blowfly (Godfray & Blythe 1990) and (b) a 144-year biweekly time series of the volume of the Great Salt Lake, Utah (Sangoyomi et al. 1996). A reliable value of the correlation dimension isn't very apparent. Other comments follow in the section ''Practical considerations and problems", below.
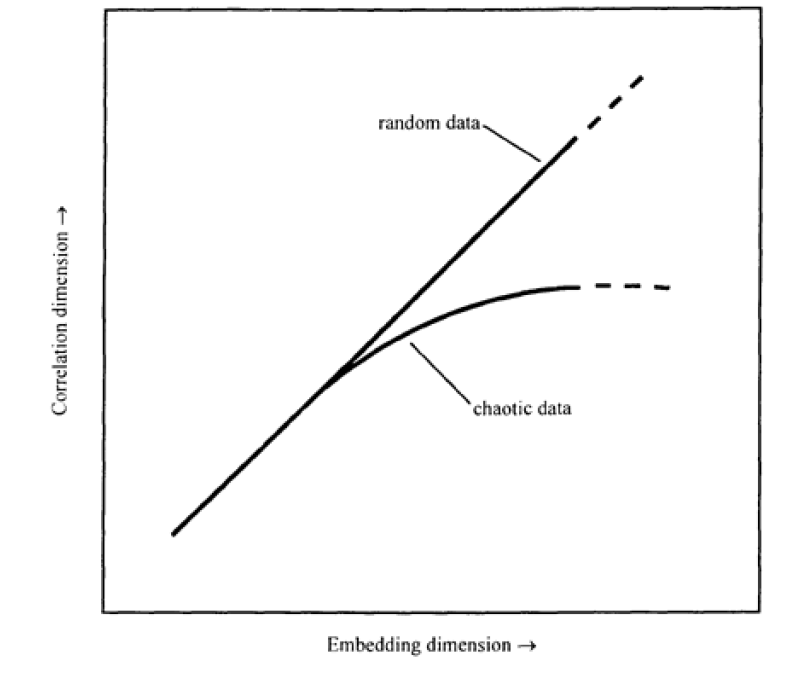
Figure 3: Hypothetical behavior (on arithmetic scales) of correlation dimension with increase in embedding dimension, for chaotic as compared to random data.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ناسا تكتشف "مدينة مهجورة" تحت جليد القطب الشمالي
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|