


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-4-2021
Date: 25-3-2021
Date: 8-3-2021
|
A moment 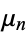 of a univariate probability density function
of a univariate probability density function 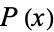 taken about the mean
taken about the mean 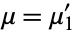 ,
,
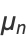 |
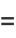 |
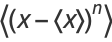 |
(1) |
 |
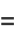 |
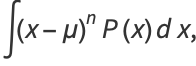 |
(2) |
where 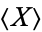 denotes the expectation value. The central moments
denotes the expectation value. The central moments 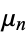 can be expressed as terms of the raw moments
can be expressed as terms of the raw moments 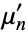 (i.e., those taken about zero) using the binomial transform
(i.e., those taken about zero) using the binomial transform
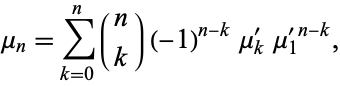 |
(3) |
with 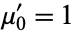 (Papoulis 1984, p. 146). The first few central moments expressed in terms of the raw moments are therefore
(Papoulis 1984, p. 146). The first few central moments expressed in terms of the raw moments are therefore
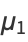 |
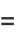 |
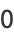 |
(4) |
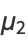 |
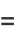 |
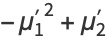 |
(5) |
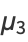 |
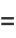 |
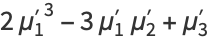 |
(6) |
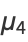 |
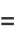 |
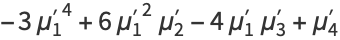 |
(7) |
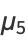 |
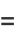 |
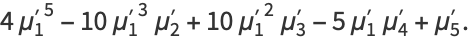 |
(8) |
These transformations can be obtained using CentralToRaw[n] in the Mathematica application package mathStatica.
The central moments 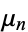 can also be expressed in terms of the cumulants
can also be expressed in terms of the cumulants 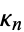 , with the first few cases given by
, with the first few cases given by
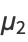 |
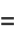 |
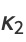 |
(9) |
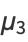 |
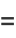 |
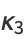 |
(10) |
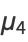 |
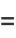 |
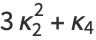 |
(11) |
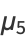 |
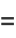 |
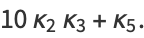 |
(12) |
These transformations can be obtained using CentralToCumulant[n] in the Mathematica application package mathStatica.
The central moment of a multivariate probability density function 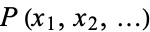 can be similarly defined as
can be similarly defined as
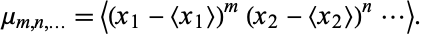 |
(13) |
Therefore,
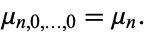 |
(14) |
For example,
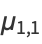 |
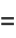 |
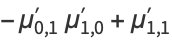 |
(15) |
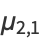 |
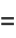 |
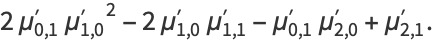 |
(16) |
Similarly, the multivariate central moments can be expressed in terms of the multivariate cumulants. For example,
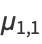 |
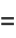 |
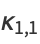 |
(17) |
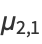 |
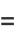 |
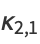 |
(18) |
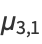 |
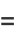 |
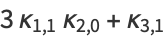 |
(19) |
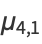 |
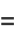 |
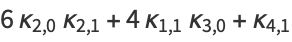 |
(20) |
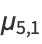 |
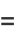 |
![15kappa_(1,1)kappa_(2,0)^2+10kappa_(2,1)kappa_(3,0)+10kappa_(2,0)kappa_(3,1)+5kappa_(1,1)kappa_(4,0)]+kappa_(5,1).](https://mathworld.wolfram.com/images/equations/CentralMoment/Inline64.gif) |
(21) |
These transformations can be obtained using CentralToRaw[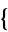 m, n, ...
m, n, ...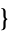 ] in the Mathematica application package mathStatica and CentralToCumulant[
] in the Mathematica application package mathStatica and CentralToCumulant[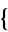 m, n, ...
m, n, ...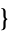 ], respectively.
], respectively.
REFERENCES:
Kendall, M. G. "The Derivation of Multivariate Sampling Formulae from Univariate Formulae by Symbolic Operation." Ann. Eugenics 10, 392-402, 1940.
Kenney, J. F. and Keeping, E. S. "Moments About the Mean." §7.3 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 92-93, 1962.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 146, 1984.
Smith, P. J. "A Recursive Formulation of the Old Problem of Obtaining Moments from Cumulants and Vice Versa." Amer. Stat. 49, 217-218, 1995



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|