


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-2-2021
Date: 8-4-2021
Date: 26-4-2021
|
A Markov chain is collection of random variables 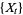 (where the index
(where the index 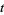 runs through 0, 1, ...) having the property that, given the present, the future is conditionally independent of the past.
runs through 0, 1, ...) having the property that, given the present, the future is conditionally independent of the past.
In other words,
 |
If a Markov sequence of random variates 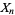 take the discrete values
take the discrete values 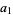 , ...,
, ..., 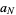 , then
, then
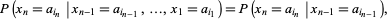 |
and the sequence 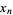 is called a Markov chain (Papoulis 1984, p. 532).
is called a Markov chain (Papoulis 1984, p. 532).
A simple random walk is an example of a Markov chain.
The Season 1 episode "Man Hunt" (2005) of the television crime drama NUMB3RS features Markov chains.
REFERENCES:
Gamerman, D. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. Boca Raton, FL: CRC Press, 1997.
Gilks, W. R.; Richardson, S.; and Spiegelhalter, D. J. (Eds.). Markov Chain Monte Carlo in Practice. Boca Raton, FL: Chapman & Hall, 1996.
Grimmett, G. and Stirzaker, D. Probability and Random Processes, 2nd ed. Oxford, England: Oxford University Press, 1992.
Harary, F. Graph Theory. Reading, MA: Addison-Wesley, p. 6, 1994.
Kallenberg, O. Foundations of Modern Probability. New York: Springer-Verlag, 1997.
Kemeny, J. G. and Snell, J. L. Finite Markov Chains. New York: Springer-Verlag, 1976.
Papoulis, A. "Brownian Movement and Markoff Processes." Ch. 15 in Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 515-553, 1984.
Stewart, W. J. Introduction to the Numerical Solution of Markov Chains. Princeton, NJ: Princeton University Press, 1995.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|